Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 123
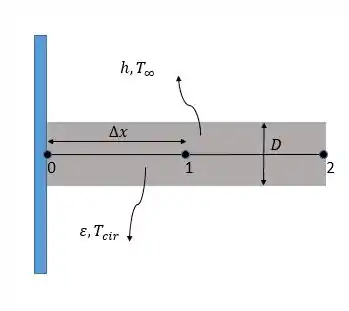
Considere a condução de calor permanente unidimensional em uma aleta do tipo pino com diâmetro constante D e condutividade térmica constante. A aleta perde calor por convecção para o ar ambiente a (em ) com coeficiente de convecção e por radiação para as superfícies envolventes a uma temperatura média de (em ). A rede nodal da aleta consiste dos nós (na base), (no meio) e (na ponta da aleta), com espaçamento nodal uniforme de . Usando a abordagem do balanço de energia, obtenha a formulação de diferenças finitas deste problema para o caso de temperatura especificada na base de aleta e transferência de calor por convecção e radiação na sua ponta.
Passo 1
Primeiramente, podemos assumir algumas condições que nos ajudam a simplificar o problema. São esses:
- Condutividade térmica constante
- Transmissão de calor através da aleta em regime permanente;
- Coeficiente de transferência de calor por convecção e emissividade são constantes e uniformes;
De posse dessas considerações, parte-se para a análise de como resolver o problema.
Passo 2
A rede nodal consiste de nós, e a temperatura no nó é especificada. Então, existem duas temperaturas desconhecidas, e , e são necessárias duas equações para determina-las. Usando a abordagem do balanço de energia, como pedido na questão, e tomando todas as transferências de calor na direção do nó sob consideração, a formulação de diferenças finitas fica da seguinte maneira:
Nó interior ():
No nó na ponta da aleta ():
Onde representa a área da seção transversal da aleta e é o perímetro correspondente à essa área de seção transversal.
Resposta
Ei, a resposta está no passo a passo :)