Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 31

Considere a condução de calor permanente unidimensional em uma parede plana com geração de calor e condutividade térmica variáveis. A rede nodal do meio consiste em nós 0, 1 e 2, com espaçamento nodal uniforme de ∆ x . Utilizando a abordagem do balanço de energia, obtenha a formulação de diferenças finitas desse problema para o caso de fluxo de calor especificado q ˙ 0 para parede e convecção no contorno à esquerda (nó 0), com coeficiente de convecção h , temperatura ambiente de T ∞ , radiação no contorno à direita (nó 2), emissividade ε e temperatura em torno da superfície T c i r .

Passo 1

Para esse exercício precisamos identificar o que está ocorrendo para aplicar o balanço de energia, então fiz uma representação aqui para termos uma melhor visualização.

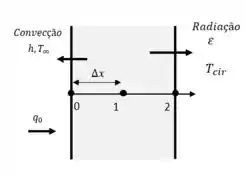
Note que há a ocorrência de fluxo térmico, calor pré-inscrito, convecção e radiação, logo precisamos considera-los no nosso equacionamento...

Passo 2

Temos que para o N ó   0 :

q ˙ 0 A + h A T ∞ - T 0 + k 0 A T 1 - T 0 ∆ x + e ˙ 0 A ∆ x 2 = 0

Para o N ó   1 :

k 1 A T 0 - T 1 ∆ x + k 1 A T 2 - T 1 ∆ x + e ˙ 1 A ∆ x 2 = 0

Para o N ó   2 :

ε σ A T c i r 4 - T 2 4 + k 2 A T 1 - T 2 ∆ x + e ˙ 2 A ∆ x 2 = 0

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro