Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 30

Considere uma parede plana grande de espessura L = 0,3   m , condutividade térmica k = 1,8 W m ∙ K e área de superfície A = 24   m 2 . O lado esquerdo da parede é submetido ao fluxo de calor q ˙ 0 = 350 W m 2 , enquanto a temperatura da superfície é medida como T 0 = 60 ° C . Pressupondo uma transferência de calor permanente unidimensional e um espaçamento nodal de 6   c m , ( a ) obtenha a formulação de diferenças finitas para os seis nós e ( b ) determine a temperatura da outra superfície da parede resolvendo essas equações.

Passo 1

Vamos lá... como primeiro passo nós vamos calcular o número de nós a partir do espaçamento nodal indicado no enunciado de ∆ x = 0,06   m .

M = L ∆ x + 1 = 0,3 m 0,06   c m + 1 = 6

Logo fazendo uma representação do problema com a quantidade de nós encontrada...

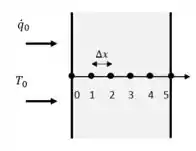
Note que a temperatura da superfície esquerda é de T 0 = 60 ° C .

Formulando a equação geral de diferenças finitas para os nós interiores 1, 2,3 e 4:

T m - 1 - 2 T m + T m + 1 ∆ x 2 + e ˙ m k = 0

Como não geração de calor.

e ˙ m k = 0

Passo 2

Logo, para o nó 0 basta aplicarmos um balanço de energia e aplicarmos a equação geral nos nós 1, 2, 3 e 4.

Para o N ó   0 :

q ˙ 0 + k T 1 - T 0 ∆ x = 0

350 W m 2 + 1,8 W m ° C T 1 - 60 ° 0,06   m = 0

T 1 = 48,3 ° C

Para o N ó   1 :

T 0 - 2 T 1 + T 2 = 0

T 2 = 2 T 1 - T 0 = 2 × 48,3 - 60

T 2 = 36,6 ° C

Para o N ó   2 :

T 1 - 2 T 2 + T 3 = 0

T 3 = 2 T 3 - T 1 = 2 × 36,6 - 48,3

T 2 = 24,9 ° C

Para o N ó   3 :

T 2 - 2 T 3 + T 4 = 0

T 4 = 2 T 3 - T 2 = 2 × 24,9 - 36,6

T 2 = 13,2 ° C

Para o N ó   4 :

T 3 - 2 T 4 + T 5 = 0

T 5 = 2 T 4 - T 3 = 2 × 13,2 - 24,9

T 2 = 1,5 ° C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro