Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 27

Considere uma parede grande plana de espessura L = 0,4   m , condutividade térmica k = 2,3 W m ∙ K e área de superfície A = 20   m 2 . O lado esquerdo da parede é mantido a uma temperatura constante de 95 ° C , enquanto o lado direito perde calor por convecção para o ar circundante a T ∞ = 15 ° C , com coeficiente de transferência de calor h = 18 W m 2 ∙ K . Pressupondo uma transferência de calor permanente unidimensional e sendo o espaçamento nodal de 10   c m , ( a ) obtenha a formulação de diferenças finitas de todos os nós, ( b ) determine as temperaturas nodais resolvendo essas equações e ( c ) avalie a taxa de transferência de calor através da parede.

Passo 1

Recolhendo os dados do enunciado, temos que:

k = 2,3 W m ∙ K ; h = 18 W m 2 ∙ K ; T 0 = 95 ° C ; T ∞ = 15 ° C ;   ∆ x = 0,1   m

Note que o espaçamento nodal é de ∆ x = 0,1 m e com a fórmula abaixo podemos encontrar o número de espaçamentos:

M = L ∆ x + 1 = 0,4   m 0,1   m + 1 = 5

Muito bem!! Agora podemos fazer uma representação do exercício com seus respectivos pontos nodais...

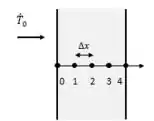
No ponto nodal 0 temos que a temperatura é T 0 = 95 ° C indicada no enunciado.

A partir da formulação para nós interiores 1, 2 e 3 podemos usar a seguinte

T m - 1 - 2 T m + T m + 1 ∆ x 2 + e ˙ m k = 0

Como não há geração de calor podemos considerar...

e ˙ m k = 0

Logo a equação se torna:

T m - 1 - 2 T m + T m + 1 = 0

Passo 2

Aplicando a equação para os nós 1, 2 e 3.

Para o N ó   1 :

T 0 - 2 T 1 + T 2 = 0

Para o N ó   2 :

T 1 - 2 T 2 + T 3 = 0

Para o N ó   3 :

T 2 - 2 T 3 + T 4 = 0

Para o N ó   4 onde temos convecção e aplicando o balanço de energia temos:

h T ∞ - T 4 + k T 3 - T 4 ∆ x = 0

Passo 3

Resolvendo as equações simultaneamente podemos chegar nas seguintes temperaturas:

T 1 = 79,8 ° C

T 2 = 64,7 ° C

T 3 = 49,5 ° C

T 4 = 34,4 ° C

Para o cálculo da taxa de transferência de calor basta usarmos a equação abaixo:

Q ˙ c o n v = h A T 4 - T ∞ = 18 W m 2 ∙ C ( 20   m 2 ) ( 34,37 - 15 ) ° C

Q ˙ c o n v = 6970   W

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro