Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 58
Reconsidere o Prob. 5–56. Usando EES (ou outro programa), investigue os efeitos da condutividade térmica e da taxa de geração de calor sobre as temperaturas dos nós 1 e 3, bem como a taxa de perda de calor a partir da superfície superior. Deixe a condutividade térmica variar de a ; varie também a geração de calor de a . Trace as temperaturas dos nós 1 e 3, bem como a taxa de perda de calor como funções de condutividade térmica e taxa de geração calor, e discuta os resultados.
Passo 1
Gerando nosso código, com os dados, a formulação de diferenças finitas e a taxa de transferência de calor. Temos que:
"DADOS"
k=150 [W/m-C] “condutividade térmica”
e_ponto=3E7 [W/m^3 “Geração de calor”
DELTAx=0.10 [m]
DELTAy=0.10 [m]
d=1 [m]
“ANÁLISE”
"(a)"
l=DELTAx
T_1=T_2 "pela simetria"
T_3=T_4 "pela simetria"
"FORMULAÇÃO DE DIFERENÇAS FINITAS”
100+120+T_2+T_3-4*T_1+(e_ponto*l^2)/k=0
150+200+T_1+T_4-4*T_3+(e_ponto*l^2)/k=0
"(b)"
-Q_ponto_sup+e_ponto*(3*l*d*l/2)+2*(k*(l*d)/2*(120-100)/l+k*l*d*(T_1-100)/l)=0
Passo 2
Gerando nossa tabela com variando de a , contendo os valores das seguintes temperaturas e taxa de transferência de calor...
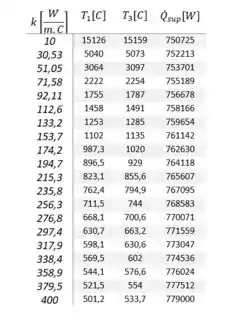
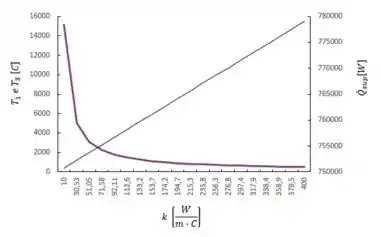
Note que com o aumento da condutividade térmica temos um decaimento da temperatura nos pontos indicados no gráfico, e que a transferência de calor se dá de forma linear.
Passo 3
Gerando nossa tabela com variando de a , contendo os valores das seguintes temperaturas e taxa de transferência de calor...
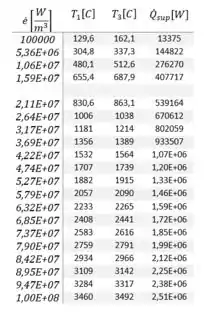
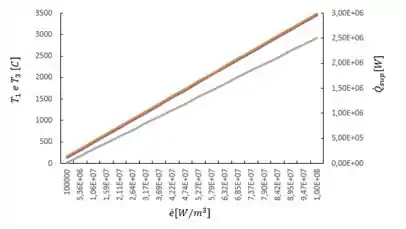
Note que com o aumento da geração de calor temos um aumento linear significativo da temperatura nos pontos indicados no gráfico, assim como um aumento linear da taxa de transferência de calor.
LINK Excel.Sheet.12 "G:\\Meu Drive\\RESPONDE AI\\Meu guia.xlsx" "Planilha2!L53C2:L72C5" \a \f 4 \h
Resposta
Ei, a resposta está no passo a passo :)