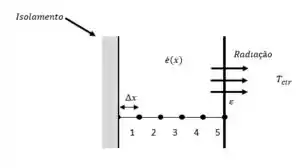
Considere uma condução de calor unidimensional permanente em uma parede plana com geração de calor variável e condutividade térmica constante. A rede nodal do meio consiste dos nós 0, 1, 2, 3, 4 e 5 com espaçamento nodal uniforme de . Usando a forma de diferenças finitas da derivada primeira (e não a abordagem do balanço de energia), obtenha a formulação de diferenças finitas dos nós de contorno para o caso de isolamento no contorno da esquerda (nó 0) e de radiação no contorno da direita (nó 5) com emissividade e temperatura ambiente de .

Então pessoal, o que precisamos encontrar primeiro aqui são as condições de contorno para os nós indicados no enunciado, vamos lá?

Note que para o nó 0 a parede se encontra isolada, logo:

Para o nó 5 segundo o exercício só ocorre radiação, e pela figura é onde termina nossa parede certo? Vamos dizer que a parede possua um comprimento , equacionando...

Lembrando que é a emissividade e é a constante de boltzmann.