Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 52
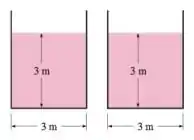
Considere o escoamento de água através de dois canais 13-52 idênticos com seções de escoamento quadradas de . Agora os dois canais são combinados, formando um canal com de largura. A vazão é ajustada para que a profundidade do escoamento permaneça constante a Determine o aumento percentual na vazão como resultado da combinação dos canais.
Passo 1
Nessa questão nós temos o fluxo de água através de dois canais idênticos com seções quadradas. Com isso vamos determinar o aumento percentual na taxa de fluxo como resultado da combinação dos dois canais enquanto a profundidade do fluxo permanece constante.
Passo 2
Para resolver essa questão vamos assumir:
- O fluxo é constante e uniforme;
- A inclinação inferior é constante;
- O coeficiente de rugosidade é constante ao longo do canal.
Vamos considerar as condições de fluxo para dois canais separados pelo subscrito e as condições para o canal amplo combinado pelo subscrito . Usando a equação de Manning,
Passo 3
Observando que o coeficiente de Manning, a inclinação do canal e a área de fluxo permanecem constantes, a vazão no caso pode ser expressa em termos de vazão no caso como,
Onde é o perímetro úmido. Substituindo,
Ou seja, houve um aumento percentual de .