Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 53
Considere o escoamento entre duas grandes placas paralelas isotérmicas separadas por uma distância . A placa superior se desloca a uma velocidade constante e é mantida a uma temperatura enquanto a placa inferior está parada e isolada. Simplificando e resolvendo as equações da continuidade, da quantidade de movimento e de energia, obtenha as relações para temperatura máxima do fluido, local em que ela ocorre e o fluxo de calor na placa superior.
Passo 1
Em primeiro lugar vamos desenhar nossa situação.
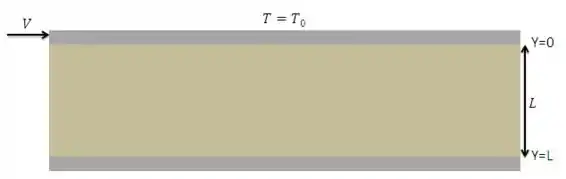
Pronto. Agora sim podemos começar. Para esse sistema o problema pede para resolver as equações de continuidade, quantidade de movimento e energia e, após isso obter a temperatura máxima, o local em que ela ocorre e o fluxo de calor na placa superior. Vamos por partes.
A equção da continuidade será nosso ponto de partida. Para o escoamento entre duas placas planas paralelas, a equação da continuidade é dada por:
Em que é a velocidade do fluido na direção e é a velocidade do fluido na direção .
Vamos assumir que o escoamento do fluido é paralelo às placas, assim, . Então:
O próximo passo é desenvolver a equação da quantidade de movimento:
Como vimos anteriormente e ; além disso, como a movimentação do fluido ocorre devido ao movimento da placa, e não devido a diferença de pressão, .
Portanto:
Integrando em y:
Integrando novamente:
Vamos agora aplicar as condições de contorno para encontrar as constantes e . Para a velocidade as condições de contorno são:
Em que é o espaçamento entre as placas. Nosso sistema de equações fica:
O perfil de velocidade é:
Passo 2
Vamos tratar agora da equação da energia. Para o escoamento entre duas placas planas paralelas a equação é:
Como e só ocorre transferência de calor na direção :
Portanto ficamos com:
Temos condições de calcular :
Substituindo no balanço de energia:
Integrando em :
Integrando em mais uma vez:
As condições de contorno são:
A primeira se refere à temperatura do mancal e a segunda condição é que o fluxo de calor pela placa inferior é zero, já que ela está isolada. Aplicando as condições de contorno:
Substituindo as constantes e no perfil de temperatura:
Com o perfil de temperatura podemos calcular o ponto de máxima temperatura. Uma breve lembrança dos tempos de cálculo: pontos de máximo ou mínimo de uma função são pontos em que a derivada . Então, o que vamos fazer é derivar em relação a e igualar a zero.
Encontramos a posição em que ocorre a temperatura máxima. Vamos agora aplicar este ponto no perfil de temperatura para encontrar a temperatura máxima do sistema:
Passo 3
Por fim, vamos determinar a taxa de transferência de calor da placa superior ():
Já calculamos a derivada de em relação a . Podemos então substituir a expressão que encontramos:
Resposta
Ei, a resposta está no passo a passo :)