Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 40
Considere o escoamento subsônico em um bocal convergente com condições de entrada fixas. Qual é o efeito da queda da contrapressão até a pressão crítica sobre (a) a velocidade de saída, (b) a pressão de saída e (c) a vazão em massa através do bocal?
Passo 1
O enunciado quer saber qual é o efeito da pressão externa da saída do bocal (também chamada de contrapressão ) sobre a velocidade do fluido na saída do bocal, sobre a pressão do fluido a saída do bocal e sobre a vazão em massa através do bocal.
A figura abaixo mostra o bocal e os dados.
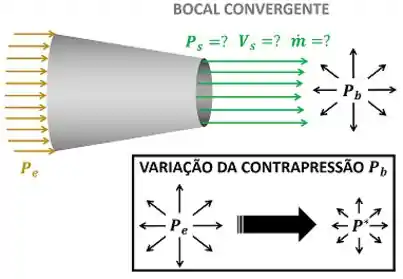
A figura acima mostra que a contrapressão cai da pressão do fluido na entrada do bocal até a pressão pressão crítica .
Explicar os efeitos dessa queda no valor da contrapressão sobre as propriedades , e é a mesma coisa que dizer se os valores dessas propriedades caem, se mantém constantes ou crescem. Além disso, precisamos saber o valor final de cada propriedade, quando .
Passo 2
Como podemos ver na figura abaixo, supomos que o bocal tem uma pressão constante na entrada.
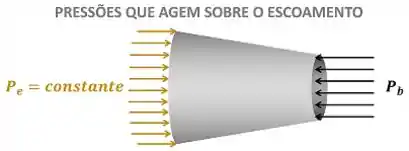
Através da imagem, vemos que o escoamento através do bocal é submetido a uma pressão constante na entrada e a uma pressão em queda na saída. Isso quer dizer que, quanto menor , maior vai ser a diferença de pressão entre a entrada e a saída e maior a força resultante da pressão sobre o escoamento.
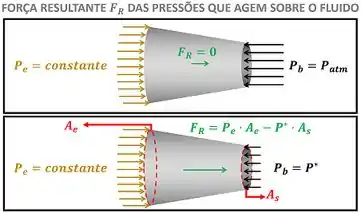
onde é a área de entrada do bocal e é a área de saída do bocal.
Ou seja, quanto menor , mais forte o escoamento do fluido através do bocal é empurrado e acelerado. Quanto mais esse escoamento é acelerado, maior sua velocidade de saída . cresce até atingir a velocidade do som .
Resumindo, quando diminui até , cresce até .
Passo 3
O efeito da queda da contrapressão sobre a pressão de saída do fluido é mais simples. A saída do bocal está em contato com o fluido externo que está a pressão . Ou seja, o fluido que está saindo do bocal com pressão está em equilíbrio com esse fluido externo a pressão . Logo, a pressão do fluido na saída é igual á pressão do fluido do lado de fora do bocal .
Isso quer dizer que quando cai até ser igual à pressão crítica , também cai até ficar igual à pressão crítica .
Passo 4
Para entender o efeito da queda da contrapressão sobre a vazão em massa do fluido, precisamos lembrar da fórmula da vazão que se encontra abaixo.
onde é a área do bocal e é a densidade do fluido.
Por essa equação nós vemos que a vazão mássica é proporcional à velocidade do fluido. Isso quer dizer que, quando a velocidade do fluido aumenta, também aumenta.
Como aumenta até um limite com a queda de , também aumenta até um limite com a queda de .