Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 48
É possível acelerar um fluido até velocidades supersônicas com uma velocidade diferente da velocidade sônica na garganta? Explique.
Passo 1
Fala, galera! Estão focados nos estudos? Que tal fazer uma questão sobre escoamento supersônico em em bocal convergente-divergente?
A questão pergunta se é possível fazer um fluido ultrapassar a velocidade do som usando um bocal convergente-divergente, se a velocidade do fluido na garganta é menor que a velocidade do som .
A figura abaixo mostra o bocal e as informações que temos para resolver a questão.
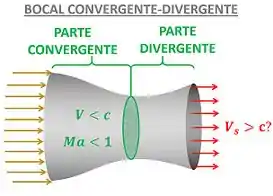
é o número de Mach na garganta. Ele é menor que , porque o enunciado quer saber o que acontece com a velocidade do fluido, quando não alcança o valor (o fluido não alcança velocidade sônica). é a velocidade do fluido na saída do bocal.
O problema quer saber então se pode ser maior que , quando é menor que .
Descobriremos a resposta usando a lei de conservação de massa na parte divergente do bocal.
Passo 2
Pela figura abaixo vemos que saber se podemos aumentar a velocidade para além da velocidade do som é o mesmo que tentar descobrir se a velocidade de saída do fluido pode ser maior que a velocidade de entrada do fluido na parte divergente do bocal.
Afinal de contas, se não consegue ser mais que , como ela será maior que ?
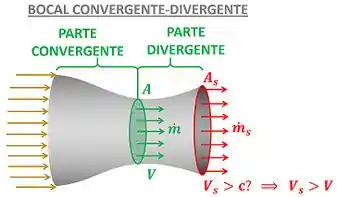
Para descobrir se , temos que usar duas equações. Uma delas é a lei da conservação de massa, que diz que a vazão mássica que entra na parte divergente tem que ser igual a vazão em massa que sai da parte divergente. A outra é a equação da vazão mássica, que diz que a vazão mássica é a multiplicação entre , e .
onde é a densidade do fluido entrando na parte divergente, é a densidade do fluido saindo da parte divergente, é a área de entrada da parte divergente (área menor), é a área de saída da parte divergente (área maior), é a velocidade de entrada do fluido e é a velocidade de saída do fluido.
Reorganizando a equação acima, encontramos uma expressão para a velocidade .
Como a área de entrada é menor que a área de saída , é menor que . Isso significa que a velocidade diminui confome o fluido atravessa o parte divergente do bocal. Em outras palavras, não aumenta e não consegue ultrapassar a velocidade do som pro escoamento virar supersônico.
Resposta
não aumenta e não consegue ultrapassar a velocidade do som pro escoamento virar supersônico, como é observado na equação de conservação de massa aplicada á parte divergente do bocal.