Considere o escoamento de gás através de um bocal convergente com condições de entrada especificadas. Sabemos que a velocidade mais alta que o fluido pode atingir na saída do bocal é a velocidade sônica, ponto em que a vazão em massa através do bocal é máxima. Se fosse possível atingir velocidades hipersônicas na saída do bocal, como isso afetaria a vazão em massa através do bocal?
Passo 1
O problema quer saber o que aconteceria com a vazão mássica do escoamento através de um bocal se a gente pudesse aumentar a velocidade do fluido na saída do bocal acima da velocidade do som . Em outras palavras, a questão quer saber o que aconteceia com se aumentássemos muito . A imagem abaixo mostra o bocal.
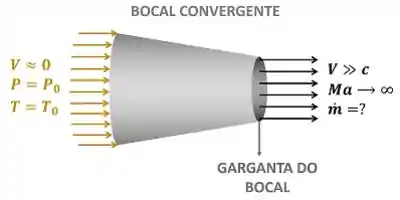
A imagem acima mostra que consideramos a velocidade de entrada do fluido no bocal aproximadamente nula. Substituindo essa informação (de ) nas fórmulas de pressão de estagnação e temperatura de estagnação , achamos que:
Isso significa que a pressão do fluido na entrada é igual à pressão de estagnação e que a temperatura do fluido é igual à temperatura de estagnação .
No próximo passo vamos começar a descobrir o que acontece com , quando aumentamos , mantendo e constantes.
Passo 2
A pergunta que o enunciado nos faz é: qual é o limite de se fizermos tender ao infinito, mantendo a pressão de estagnação e a temperatura de estagnação constantes? Em outras palavras esse é um problema de limite!
Para responder isso, temos que usar a equação da vazão mássica através do bocal convergente em função do número de Mach (equação 12-24 do livro).
onde é a área da garganta do bocal, é a razão de calores específicos do fluido e é a constante de gás do fluido.
Substituindo essa expressão no limite, achamos:
Passo 3
Podemos notar olhando para o limite que o número de Mach está presente tanto no numerador quanto no denominador. Isso significa que, a primeira vista, esse limite leva a uma indeterminação do tipo , porque tanto o numerador quanto o numerador tendem ao infinito, quando tende ao infinito
Como essa indeterminação aparece nesse limite, podemos aplicar a Regra de l’Hôpital e achar esse limite derivando o numerador e o denominador em relação a .
Substuindo as derivadas no limite, ele se torna:
Agora só tem no denominador. Como tende ao infinito, essa divisão tente a zero. Logo, o limite tende a zero.
Em outras palavras, se a velocidade do fluido que está saindo do bocal crescer para além da velocidade do som , a vazão mássica diminui e no caso limite (quando a velocidade do lfuido cresce muito), tende a zero!
Resposta
Se a velocidade do fluido que está saindo do bocal crescer para além da velocidade do som , a vazão mássica diminui e no caso limite (quando a velocidade do lfuido cresce muito), tende a zero!