Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 6
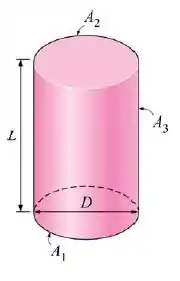
Considere um invólucro cilindro com A1, A2 e A3, representando as bases interas e superior e as superfícies lateriais, respectivamente. Usando a razão de comprimento de diâmetro K = L/D, determina (a) a expressão para o fator de forma entre a base e a superfície lateral F13 em K e (b) o valor do fator de forma de F13 para L = D
Passo 1
(a) Vamos começar aplicando a regra do somatório, se liga!
Onde a gente sabe que
Chegamos então a
Passo 2
Na tabela 13-1 do Çengel você vai encontrar que para discos paralelos coaxiais para os índices i=1 e j=2 a seguinte relação para fator de forma:
Como D1 = D2 porque estamos vendo as “tampas” do mesmo cilindro,
Ainda usando dados da tabela:
Sabendo que R1 = R2 = R = D/2L = 1/2K
Passo 3
Bora substituir essa última equação na equação de
Agora a gente pega essa equação e subsitui na equação lá de cima que começamos o problema!!
Passo 4
(b) Agora é só fazermos L=D supondo que K=1 (para facilitar nossa vida rsrs)
Resposta
Ei, a resposta está no passo a passo :)