Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 18
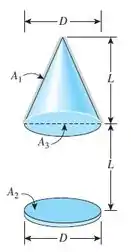
Um cone circular de diâmetro D é posicionado em um eixo comum com disco circular, também de diâmetro, D, a uma distância L, como mostrado na Fig. P13-18. Com uma área hipotética correspondente à abertura do cone, determine os valores de e para mm.
Passo 1
Animados para continuar??
Então vamos começar ...
Bom, se nós queremos o fator de forma podemos começar usando a regra do somatório, considerando as superfícies 1 e 3, ok?
Uma relação muito importante que poderemos usar aqui é:
Então, para nós sabermos o antes precisamos achar o . E como faremos?
Podemos usar a relação da reciprocidade para chegar mais perto do que queremos:
Isolando:
Vamos começar achando as áreas?
Substituindo os valores de L e D:
Na fórmula:
Este dado nós podemos lançar para achar o fator de forma 11, ok?
Passo 2
Mas isso ainda não resolveu nada, não é?
Só que podemos achar o fator de forma usando o somatório para a superfície 3:
O fator de superfície 3-3:
Então:
Colocando na fórmula que achamos no Passo 1:
Olha que legal, já achamos uma resposta !!
Passo 3
Agora nós precisamos achar para isso nós podemos usar a relação da reciprocidade:
Isolando:
Na fórmula:
Como a radiação saindo da superfície 2 e atingindo 1 é igual a radiação saindo de 2 e atingindo 3:
Então, se acharmos poderemos achar !
E para isso basta nós usarmos a relação para dois discos paralelos:
Se:
Então:
Sendo assim nós só precisamos de achar o S, certo?
Passo 4
Para achar o S de dois discos concêntricos:
Se:
O problema nos disse que:
Substituindo:
Achando o nosso S:
Agora vamos colocar na fórmula para achar
E com isso nós achamos o que? Acertou quem disse o
Legal, não foi ?!