39 – Considere uma panela de alumínio usada para cozinhar um ensopado no fogão elétrico. A seção inferior da panela tem espessura e diâmetro . Uma boca do fogão consome de potência durante seu uso, e 90% do calor gerado é transferido uniformemente para a panela. Durante a operação permanente, a temperatura da superfície interna da panela é de . Assumindo a transferência de calor unidimensional e condutividade térmica dependente da temperatura, expresse a formulação matemática (equação diferencial e condições de contorno) desse problema de condução de calor durante a operação permanente. Não resolva.
Passo 1
Considere a transferência de calor através da bandeja de espessura L com condutividade térmica variável, como mostrado:
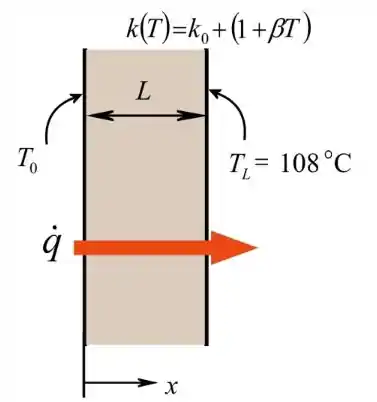
Aqui, está a temperatura em , é a temperatura em , é o fluxo de calor através da panela e é a condutividade térmica variável com a temperatura.
Passo 2
Vamos escrever a equação geral de condução de calor.
Aqui, é a densidade do corpo considerada, é o calor específico, é o gradiente de temperatura em relação ao tempo, ![]()
Passo 3
Aqui, a panela é unidimensional, constante, sem geração interna de calor e a condutividade térmica varia com a temperatura.
A equação se reduz a,
Aqui está a condutividade térmica média e é a constante de integração.
A condutividade térmica média é dada por,
A equação diferencial governante é
Passo 4
Escreva as condições de contorno do sistema. Onde ,
Temos que: e
Aqui é a temperatura de superfície interna da panela.
Portanto, as condições de contorno para o problema de condução de calor durante o estado estacionário são
Passo 5
Calcule a área da superfície da panela.
Agora conseguimos calcular o fluxo de calor na parte inferior da panela com a seguinte relação:
Aqui é a taxa de transferência de calor, a eficiência, o fluxo de calor no fundo da panela, a potência durante o cozimento e a área da seção transversal da panela.
Substituindo , e
Portanto, o fluxo de calor no fundo da panela é .
Resposta
Portanto, o fluxo de calor no fundo da panela é .