Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 9
9 – Um vetor de fluxo de calor em um ponto P na superfície isotérmica de um meio é necessariamente perpendicular à superfície nesse ponto? Justifique.
Passo 1
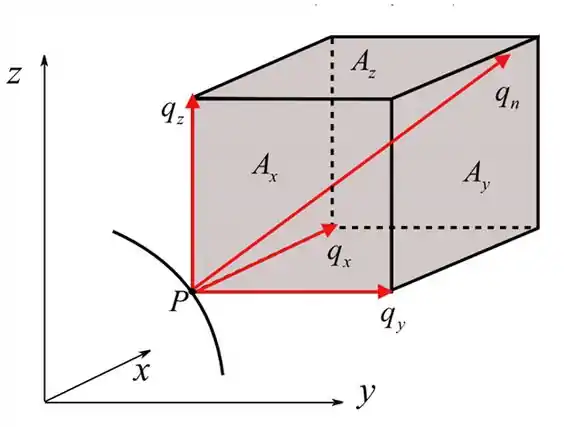
Considere uma superfície isotérmica em um meio, em que a distribuição de temperatura é tridimensional.
Passo 2
O fluxo de calor no ponto P pode ser expresso pela lei de Fourier.
Aqui, é o fluxo de calor, é a condutividade térmica, é a temperatura, é a direção normal da superfície isotérmica e é o gradiente de temperatura.
Na superfície isotérmica, o gradiente de temperatura é zero ao longo da superfície, e o gradiente de temperatura está presente apenas na direção normal da superfície isotérmica. Portanto, não há fluxo de calor ao longo da superfície, mas existe um fluxo de calor perpendicular à superfície isotérmica, que pode ser resolvido em seus componentes como qualquer outro vetor e deve apontar na direção da diminuição da temperatura.
Resposta
Não há fluxo de calor ao longo da superfície, mas existe um fluxo de calor perpendicular à superfície isotérmica, que pode ser resolvido em seus componentes como qualquer outro vetor e deve apontar na direção da diminuição da temperatura.