Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 131
Considere uma parede grande plana de espessura e condutividade térmica no espaço . A parede é coberta por material com emissividade e absortividade solar . A superfície interna da parede é mantida a em todos os momentos, enquanto a superfície externa é exposta à radiação solar incidente à uma taxa de . A superfície externa também perde calor por radiação no espaço profundo a . Usando espaçamento nodal uniforme de , (a) obtenha a formulação de diferenças finitas para condução de calor constante unidimensional e (b) determine as temperaturas nodais, resolvendo as equações.
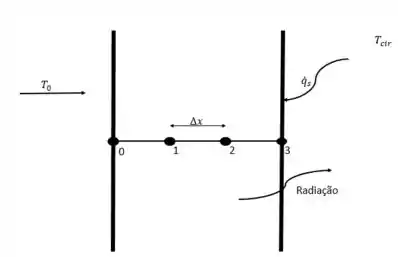
Passo 1
Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:
- O calor transferido através da parede é dado como constante e unidimensional.
- Condutividade térmica é constante.
- Não há geração de calor.
- Não há convecção no espaço.
De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.
Passo 2
(a) O número de nós é calculado da seguinte maneira:
Esse problema envolve temperaturas nodais desconhecidas, uma vez que a temperatura do nó é a temperatura da parede interna, ou seja , e isso implica em precisarmos de equações para encontrá-las. Os nós e são nós interiores, portanto para eles podemos usar a relação geral de diferenças finitas:
Desde que , então para os nós e temos o seguinte:
Nó 1:
Nó 2:
E para o nó , faz-se o balanço de energia no nó, considerando toas as transferências de calor em direção ao nó em questão:
Nó 3:
O sistema de equações com temperaturas desconhecidas constitui a formulação de diferenças finitas do problema.
Passo 3
As temperaturas nodais sob condições permanentes são determinadas pela solução das equações acima simultaneamente, e elas fornecem como resultado:
Resposta
(b)