Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 136

Uma placa de bronze quente está sendo resfriada na superfície superior por um jato de ar a uma temperatura de 15 ℃ , com coeficiente de transferência de calor por convecção de 220   W / m ² K . A espessura da placa de bronze é 10   c m ( ρ = 8530   k g / m ³ ,   C p = 380   J / k g . K ,   k = 110   W / m . K e α = 33,9 × 10 - 6   m ² / s ) com temperatura uniforme inicial de 650 ℃ e superfície inferior isolada. Usando espaçamento nodal uniforme de ∆ x = 2,5   c m , determine (a) equações de diferenças finitas explícitas, (b) valor máximo admissível de passo de tempo, (c) temperatura no centro plano da placa após 1 minuto de resfriamento, e (d) compare os resultados (c) com a solução analítica aproximada do Cap. 4.

Passo 1

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

  • Condução de calor é transitória e unidimensional.
  • Propriedades térmicas são constantes.
  • Não há geração de calor.
  • Coeficiente convectivo de transferência de calor é uniforme.
  • Transferência de calor por radiação é desprezível.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

Passo 2

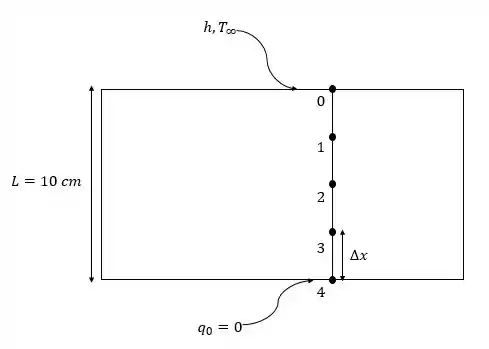
(a) O número de nós é dado por:

M = L ∆ x + 1 = 10 2,5 + 1 = 5

Como o problema envolve 5 temperaturas nodais desconhecidas, precisaremos de 5 equações para determina-las. A equação de diferenças finitas para o nó 0 no topo da placa, sujeito à convecção, é obtida através do balanço de energia em torno desse nó, considerando as transferências de calor vindas de todas as direções.

Já o nó 4 , que está numa superfície isolada, pode ser tratado como um nó interior pelo conceito de imagem do espelho, ambos se desenvolvem da seguinte forma:

Nó 0 : h T ∞ - T 0 i + k T 1 i - T 0 i ∆ x = ρ ∆ x 2 C p T 0 i + 1 - T 0 i ∆ t

Nós 1 ,   2 ,   3   e 4 : T m - 1 i - 2 T m i + T m + 1 i = T m i + 1 - T m i τ

E após explicitarmos as variáveis de interesse, temos:

Nó 0 : T 0 i + 1 = 1 - 2 τ - 2 τ h ∆ x k T 0 i + τ 2 T 1 i + 2 h ∆ x k T ∞

Nó 1 : T 1 i + 1 = τ T 0 i + T 2 i + 1 - 2 τ T 1 i

Nó 2 : T 2 i + 1 = τ T 1 i + T 3 i + 1 - 2 τ T 2 i

Nó 3 : T 3 i + 1 = τ T 2 i + T 4 i + 1 - 2 τ T 3 i

Nó 4 : T 4 i + 1 = τ T 3 i + T 3 i + 1 - 2 τ T 4 i

E as equações para cada nó são obtidas com a substituição dos dados fornecidos pela questão.

Passo 3

(b) O limite do passo de tempo ∆ t é determinado pelo critério de estabilidade que requere que todos os coeficientes primários sejam maior que 0 ou igual a 0 . O coeficiente de T 0 i é menor nesse caso, então o critério de estabilidade desse problema pode ser expresso da seguinte maneira:

1 - 2 τ - 2 τ h ∆ x k ≥ 0 → τ ≤ 1 2 1 + h ∆ x k → ∆ t ≤ ∆ x 2 2 α 1 + h ∆ x k

E após substituirmos os valores fornecidos, o valor máximo permitido para o passo de tempo é:

∆ t ≤ 0,025   m 2 2 33,9 × 10 - 6   m 2 / s 1 + 220   W / m 2 K 0,025   m 110   W / m . K = 8,779   s

Então, qualquer passo de tempo menor que 8,779   s pode ser utilizado. Para trabalharmos, vamos escolher ∆ t = 6   s . Então, o número de Fourier fica:

τ = α ∆ t ∆ x ² = 33,9 × 10 - 6   m 2 / s ( 6   s ) ( 0,025   m ) ² = 0,32544

Passo 4

(c) Com as temperaturas nodais iniciais de 650 ℃ , os resultados obtidos nas iterações são listados na tabela a seguir:

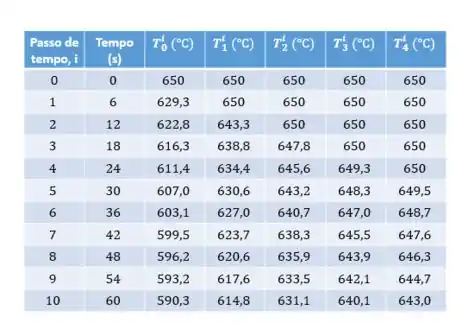
Então, a temperatura do centro plano da placa de bronze após 1   m i n de resfriamento é:

T 2 10 = 631,1 ℃

Passo 5

(d) No capítulo 4 , a solução analítica aproximada é dada da seguinte maneira:

θ p a r e d e = T x , t - T ∞ T i - T ∞ = A 1 e - λ 1 2 τ cos ⁡ λ 1 x L

Sabendo que B i = h L / k = 0,2 e τ = α ∆ t / ∆ x ² = 0,2034 > 0,2 , e da tabela 4-2 obtém-se A 1 = 1,0311 e λ 1 = 0,4328 , então, consequentemente:

T x , t = T i - T ∞ A 1 e - λ 1 2 τ cos ⁡ λ 1 x L + T ∞

T 0,05   m ,   180   s = ( 650 ℃ - 15 ℃ ) ( 1,0311 ) e - ( 0,4328 ) ² ( 0,2034 ) cos ⁡ 0,4328 ( 0,5 ) + 15 ℃

= 630 ℃

A diferença entre a solução numérica e a analítica aproximada é em torno de ∓ 8 % .

Resposta

b   ∆ t ≤ 8,779   s

c   T 2 10 = 631,1 ℃

d   T 2 30 = 630,6 ℃

Ver Outros Exercícios desse livro