Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 90

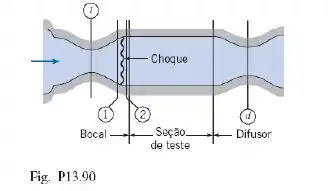
Considere a partida de um túnel de vento supersônico conforme mostrado. A área da garganta do bocal é 0,12   m ² , e o número de Mach de projeto na seção de teste é 2,50 . Conforme o túnel começa a funcionar, ocorre um choque normal na parte divergente do bocal onde a área é 0,28   m ² . As condições de estagnação a montante são T 0   =   600   K e p 0   =   790   k P a   ( a b s ) . Determine a mínima área de garganta do difusor teoricamente possível nesse instante. Calcule o aumento de entropia através do choque.

Passo 1

Fala aí galera, bora pra mais uma questão de Mecânica dos fluidos para tirarmos aquele notão na prova. Primeiramente, temos que (Ap E.1):

M 1 = 2,416 → A 1 A t = 2,44

Também temos que (Ap E.4):

M 1 = 2,416 → p 02 p 01 = 0,5395

Logo:

p 01 = 427,47   k P a

Para um escoamento adiabático:

T 0 = c t e → T * = T 0 1,2 = 500 K

Usando a equação da continuidade:

m ˙ = ρ t A t V t = ρ d V d A d

Substituindo ρ = p R T   e V = M k R T :

p t R T t k R T t A t = p d R T d k R T d A d

A d = A t p t p d = 0,215 m 2

Passo 2

Agora, vamos usar a equação de Gibbs:

T   d s = d h - v d p

d s = C p d T T - R d p p

∆ s = C p ln ⁡ T 02 T 01 - R ln ⁡ p 02 p 01

Como T 0 = c t e :

∆ s = 81,12 k J / k g f

Resposta

A d = A t p t p d = 0,215 m 2

∆ s = 81,12 k J / k g f

Ver Outros Exercícios desse livro