Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 73
Considere um pedaço de aço que passa por um processo de descarburação a 925°C. A difusividade de massa de carbono no aço a 925°C é de . Determine a profundidade abaixo da superfície do aço na qual a concentração de carbono é reduzida em 40% do seu valor inicial como resultado do processo de descarburação (a) por uma hora e (b) dez horas. Suponha que a concentração de carbono na superfície seja zero durante todo o processo de descarburação.
Passo 1
Bora continuar?
Então galera, o que temos aqui?
Nós temos as frações mássicas da espécie A em questão, certo? Temos que achar a profundidade em um determinado intervalo de tempo. Sendo assim, nós podemos usar uma fórmula que vai nos ajudar demaaais:
Se reduzimos 40% do seu valor inicial:
Reorganizando:
O que mais sabemos?
Substituindo:
Passo 2
Na letra (a) nós temos que:
Agora nós vamos só substituir na fórmula do Passo 1:
Para achar a função erfc vamos ter que interpolar galera!
Olhem nossa tabelinha aí:
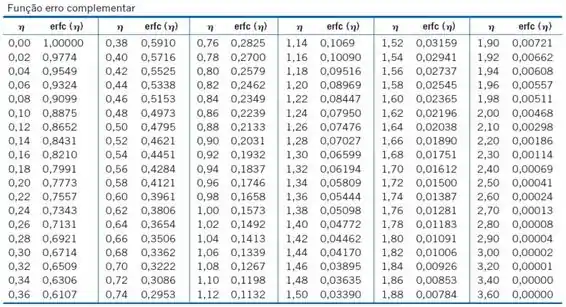
Como
Se lembram da interpolação?
Substituindo:
Se é assim:
Passo 3
Na letra (b) nós temos que:
Na letra (a) nós temos que:
Agora nós vamos só substituir na fórmula do Passo 1:
Já sabemos que:
Tranquilinha, não foi?