Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 52

Considere uma transferência de calor permanente bidimensional em duas longas barras solidas cujas seções transversais são dadas na Fig. P5–52. As temperaturas medidas nos pontos selecionados das superfícies externas são mostradas. A condutividade térmica do corpo é k = 20 W m ∙ K , e não há geração de calor. Usando o método de diferença finita com malha uniforme de ∆ x = ∆ y = 1,0   c m , determine as temperaturas nos pontos indicados no meio. Dica: tire proveito da simetria.

( a )

( b )

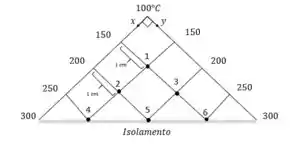
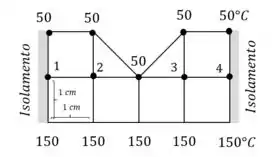
Passo 1

Temos aqui um problema de condução de calor bidimensional em regime permanente, logo a formulação para esse caso é:

T e s q + T s u p + T d i r + T i n f - 4 T n ó + e ˙ n ó l 2 k = 0

Como não temos geração de calor, a equação se torna:

T e s q + T s u p + T d i r + T i n f - 4 T n ó = 0

Passo 2

( a ) Note que o desenho é simétrico, e podemos aproveitar isso em nossas equações em cada ponto nodal.

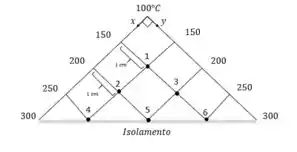
A partir da simetria temos que T 3 = T 2 e T 6 = T 4 .

Portanto nossas equações ficaram...

N ó   1 :

150 + 150 + 2 T 2 - 4 T 1 = 0

N ó   2 :

200 + T 1 + T 5 + T 4 - 4 T 2 = 0

N ó   4 :

250 + 250 + T 2 + T 2 - 4 T 4 = 0

N ó   5 :

4 T 2 - 4 T 5 = 0

Resolvendo as equações simultaneamente temos:

T 1 = 175 ° C

T 2 = T 3 = 200 ° C

T 4 = T 6 = 225 ° C

T 5 = 200 ° C

Passo 3

b Utilizando uma linha de simetria vertical, temos que T 3 = T 2   e   T 4 = T 1 .

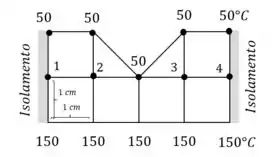
Aplicando a equação...

N ó   1 :

50 + 150 + 2 T 2 - 4 T 1 = 0

N ó   2 :

50 + 50 + 150 + T 1 - 4 T 2 = 0

Resolvendo as equações simultaneamente encontramos:

T 1 = T 4 = 92,9 ° C

T 2 = T 3 = 85,7 ° C

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro