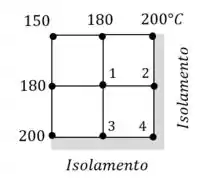
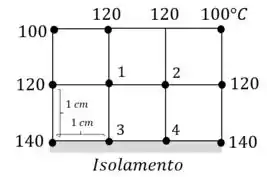
Considere uma transferência de calor permanente bidimensional em longas barras solidas de seções transversais quadrada e retangular, como mostrado na Fig. P5–54. As temperaturas medidas nos pontos selecionados da superfície externa são mostradas. A condutividade térmica do corpo é , e não há geração de calor. Usando o método de diferenças finitas com tamanho da malha de, determine as temperaturas do meio nos pontos indicados.

Note que por simetria temos que . Portanto precisamos equacionar somente os seguintes nós...

:

:

:

Resolvendo as equações, as temperaturas são:

A partir da simetria temos que e . Equacionando para cada nó:

:

:

:

Logo as temperaturas são...