Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 5.Problemas - Ex. 134
Considere uma transferência de calor permanente bidimensional em uma longa barra sólida () de seção transversal quadrada (), com calor gerado na barra de maneira uniforme a uma taxa de . As superfícies da esquerda e inferior mantém temperatura constante de . As superfícies inferior e direita são submetidas à convecção com temperatura do ar ambiente de e coeficiente de transferência de calor de . Usando um tamanho de malha uniforme centímetro, determine (a) equações de diferenças finitas e (b) temperaturas nodais com método iterativo de Gauss-Seidel.
Passo 1
Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:
- Condução de calor é permanente e bidimensional.
- Propriedades térmicas são constantes.
- A geração de calor no corpo é uniforme.
De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.
Passo 2
(a) Existe um eixo de simetria na diagonal que passa pelos nós e , então . Dessa maneira, temos temperaturas desconhecidas ( e ) e precisaremos de equações para encontra-las:
Nó 1:
Nó 2:
Nó 3:
E após explicitarmos as variáveis de interesse e substituirmos os dados fornecidos, temos:
Nó 1:
Nó 2:
Nó 3:
Passo 3
(b) O método de Gauss-Seidel necessita de chutas iniciais para cada uma das variáveis que estão sendo analisadas, e como temos variáveis, deixaremos como chutes iniciais , e os resultados gerados pelas iterações estão listados abaixo:
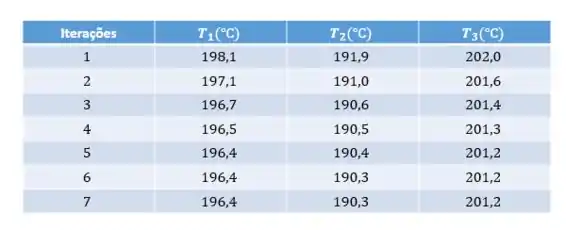
E após a convergência, verifica-se que as temperaturas valem: