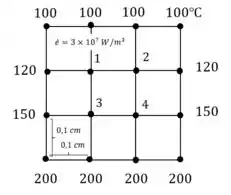
Considere uma transferência de calor permanente bidimensional em um longo corpo sólido cuja seção transversal é dada na Fig. P5–56. As temperaturas dos nós selecionados e as condições térmicas nos contornos são mostradas. A condutividade térmica do corpo é e o calor é gerado no corpo uniformemente a uma taxa de . Usando o método das diferenças finitas com tamanho de malha de, determine as temperaturas dos nós 1, 2, 3 e 4 e a taxa de perda de calor na superfície superior através da seção do corpo de de comprimento.

Logo precisamos somente de duas equações para encontrar nossas temperaturas. Sendo elas:

:

:

Utilizando de nossas igualdades, as equações se tornam:

Resolvendo as equações simultaneamente, as temperaturas são...

Podemos encontrar a taxa e transferência de calor superior com profundidade de , aplicando um balanço de energia: