Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 25
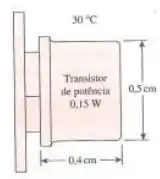
Considere um transistor de potência que dissipe 0,15 W de potência em um ambiente a 30 °C. O transistor tem 0,4 cm de comprimento e diâmetro de 0,5 cm. Pressupondo que o calor é transferido uniformemente de todas as superfícies, determine (a) a quantidade de calor que esse transistor dissipa durante o período de 24 horas, em kWh, (b) o fluxo de calor na superfície do transistor, em , e (c) a temperatura da superfície do transistor para o coeficiente combinado de transferência de calor por convecção e por radiação de .
Passo 1
Nosso ponto de partida é colocar as hipóteses do nosso problema. São elas que possibilitam a sua solução!
Portanto, temos um problema de transferência de calor em regime permanente, unidimensional e condutividade térmica constante.
Primeiramente, vamos calcular a quantidade de calor dissipado no período de 24 horas. E isto é bem simples. A questão não nos forneceu a taxa de calor dissipado (0,15 W)? Então, basta multiplicarmos este valor pelo tempo! Logo,
Respondendo então a letra a).
Passo 2
Já na letra b) queremos determinar o fluxo de calor na superfície do transistor. Como estamos em regime permanente, não há acumulo de calor no corpo. Isto significa que todo o calor gerado é dissipado 100%.
Então, vamos primeiramente calcular a superfície do transistor (lateral + superior + inferior). Portanto,
Desta forma, o fluxo na superfície do transistor é:
Passo 3
Por fim, vamos determinar a temperatura na superfície do transistor. Como todo o calor é dissipado por convecção, basta aplicarmos a equação da transferência de calor por condução. Desta forma, temos:
Resposta
- A quantidade de calor dissipado é:
- O fluxo de calor na superfície é:
- A temperatura na superfície do transistor é: