Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 23
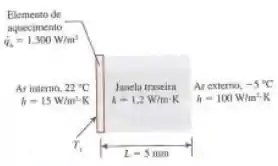
Para desembaçar a janela traseira de um automóvel, um elemento fino e transparente de aquecimento é ligado à superfície interna da janela. O fluxo de calor uniforme de é fornecido para o elemento de aquecimento desembaçar a janela traseira com espessura de 5 mm. A temperatura interior do automóvel é 22 °C, e o coeficiente de transferência de calor por convecção é . A temperatura ambiente fora está a 5 °C, e o coeficiente de transferência de calor por convecção . Considerando que a condutividade térmica da janela é , determine a temperatura da superfície interna da janela.
Passo 1
Nosso ponto de partida é colocar as hipóteses do nosso problema. São elas que possibilitam a sua solução!
Portanto, temos um problema de transferência de calor em regime permanente, unidimensional e condutividade térmica constante.
Podemos associar este problema a noção de resistências elétricas. O calor fluirá da superfície interna para a superfície interna, devido ao gradiente de temperaturas. Portanto, temos 3 elementos no nosso circuito: uma resistência de convecção da superfície interna para o vidro; uma resistência térmica de condução; e a convecção na superfície externa. Além disto, temos a presença de um fluxo adicional de calor, antes da janela.
Podemos representar esta situação através da seguinte figura:
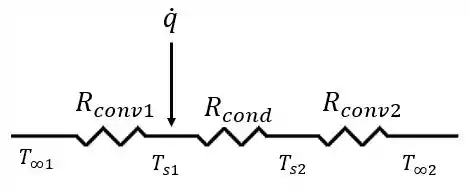
Calculando as resistências térmicas, temos:
Percebam que calculamos a resistência térmica por unidade de área pois este dado não foi fornecido na questão. Inclusive, ele não será necessário.
Agora, basta aplicarmos as fórmulas da condução para obtermos tanto a taxa de transferência de calor quanto a temperatura da superfície interna do vidro.
Passo 2
Após a primeira resistência térmica, a relacionada a convecção do ambiente interno, temos a adição de um novo fluxo de calor. Portanto, o fluxo de calor dos dois elementos seguintes é exatamente igual ao fluxo de calor na resistência somada ao fluxo adicional.
Portanto, escrevendo esta relação matematicamente, temos:
Substituindo os valores das constantes e resolvendo para , que representa a temperatura na superfície interna da janela, temos:
OBS: percebam que o texto nos diz que a temperatura externa é 5 °C, mas na figura da questão este valor é igual a -5 °C. Portanto, para os cálculos desta questão, foi utilizado o valor de -5 °C.
Resposta
A temperatura na superfície interna da janela é: