Ar está contido em um dispositivo cilindro pistão. A temperatura do ar é . Usando o fato de que, para um processo reversível, a transferência de calor é dada por , compare a quantidade de calor () necessária para elevar a temperatura do ar até na condição de (a) pressão constante e (b) volume constante. Verifique seus resultados, usando a primeira lei da termodinâmica. Trace o processo em um diagrama .
Passo 1
Vamos começar anotando todos os nossos dados pra gente não se perder, beleza?
Mas a gente precisa fazer algumas considerações, como: estar trabalhando com gás ideal e nosso calor específico ser constante.
Além disso, não podemos esquecer de anotar as nossas constantes, que já estão tabeladas de acordo com as considerações que fizemos, e que temos que observar que elas apresentam o Kelvin como unidade de temperatura então precisamos ajustar isso aí. Partiu!
Beleza! Vamos começar no próximo passo com os cálculos!
Passo 2
Bom, vamos resolver primeiro os questionamentos da letra A , que pede pra gente encontrar a quantidade de calor à pressão constante. Para isso vamos partir da seguinte relação:
E como temos o constante:
E se recordarmos que:
Aí nós ficaremos com:
Agora usando o dado do nosso enunciado, , teremos:
Show! Conseguimos!
Passo 3
Vamos agora para a letra B encontrar vazão a um volume constante:
E como temos o constante:
E se recordarmos que:
Aí nós ficaremos com:
Agora usando o dado do nosso enunciado, , teremos:
Aeee! Conseguimos! Show!
Passo 4
Agora precisamos comparar a quantidade de calor em cada um dos casos, afinal é isso que a questão quer, né?!
Bom, vemos no passo 2 e no passo 3 que a pressão constante precisamos de mais calor que no caso do volume constante.
Passo 5
Agora para plotar o gráfico de temperatura versus entropia, precisamos adequar a fórmula de entropia para as letras A e B:
Com a pressão constante, temos:
E com o volume constante, temos:
Agora sim podemos plotar nosso gráfico!
Nosso gráfico tem representado na linha vermelha o processo à volume constante e na linha azul à pressão constante.
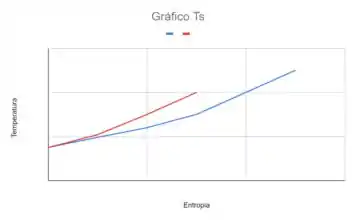
Resposta
Comparando vemos que no passo 2 e no passo 3 que a pressão constante precisamos de mais calor que no caso do volume constante.
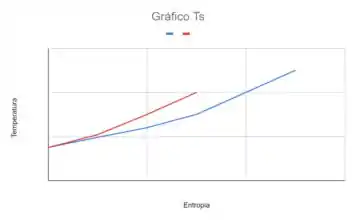
Resposta
Ei, a resposta está no passo a passo :)