Para o escoamento laminar na seção de tubo mostrada na Fig. 8.1, trace a tensão de cisalhamento de parede, a pressão e a velocidade na linha de centro como funções da distância ao longo do tubo. Explique as características significativas dos gráficos, comparando-os com o escoamento completamente desenvolvido. Pode a equação de Bernoulli ser aplicada em alguma parte do campo de escoamento? Se afirmativo, onde? Explique brevemente.
Passo 1
Tá legal! Então conforme vimos nessa seção, sabemos que há uma redução de velocidade conforme nos aproximamos da parede do escoamento, de forma que, para o escoamento longe da entrada, totalmente desenolvido, a velocidade da linha de centro é o dobro da velocidade de entrada para que a vazão seja mantida. Quando as camadas limite se juntam na linha de centro ao longo do escoamento, todo o escoamento está sujeito aos efeitos de atrito. Então, a partir disso, não podemos mais aplicar a equação de Bernoulli.
Passo 2
Quando o escoamento se torna totalmente desenvolvido, o gradiente de pressão do escoamento se torna constante, ou seja, a queda de pressão será linear. E, conforme podemos imaginar, devido a mudança das condições do escoamento, que gera grandes forças de atrito, o gradiente de pressão é maior na entrada, ou seja, a pressão cai com mais rapidez.
Passo 3
E, agora, com relação as forças de atrito, devido à mudança brusca das condições de escoamento, sabemos que a tensão de cisalhamento será grande na entrada e irá diminuir conforme as camadas limites vão se tornando maiores, até atingir um valor praticamente constante.
Passo 4
Agora vamos aos gráficos, o gráfico da relação de velocidade para a linha de centro, conforme descrito no passo 1, será:
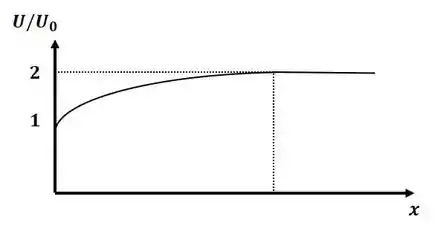
Já o grafico da pressão ao longo do escoamento, será:
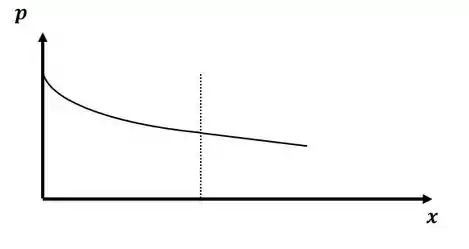
E, por fim, o gráfico da tensão de cisalhamento terá o seguinte formato:
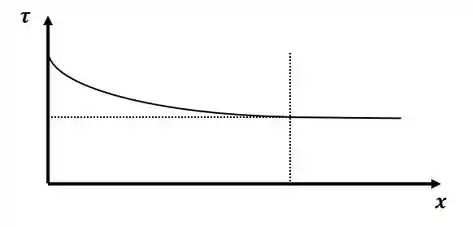
Resposta
Ei, a resposta está no passo a passo :)