Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 33
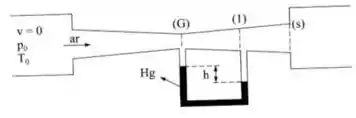
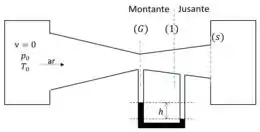
No convergente/divergente da figura, sabe-se que o escoamento imediatamente a montante da seção (1) é supersônico. Pelo desnível do manômetro diferencial, é possível afirmar que na seção indicada existe uma onda de choque? Justif6ique
Dados:
Determinar:
- O número de Mach na seção imediatamente a jusante da onda de choque;
- O número de Mach na seção de saída do bocal;
- As pressões de estagnação a montante a jusante da onda de choque.
Passo 1
Para melhor entender a situação, observe a tabela 12.1 do livro (página 354).
Sabemos que o escoamento entre (G) e (1) é supersônico! Quando um escoamento supersônico passa por um divergente sua pressão deveria diminuir, mas a leitura do manômetro indica que a pressão aumentou. Isso quer dizer que uma onda de choque aconteceu, o escoamento se tornou subsônico e sua pressão aumentou.
Passo 2
Item a)
Na Tabela 1 podemos usar a razão entre a área do ponto (1) e a área crítica à jusante do choque para determinar o número de Mach imediatamente após o choque Mas para calcular o valor de podemos utilizar a tabela 1 e os dados do fluxo de saída (s)
Agora calculamos o valor da área crítica a jusante:
Agora vamos usar os dados do ponto (1) para determinar o número de mach a jusante do ponto de choque:
Passo 3
Item b) Para determinar o número de Mach na saída do bocal podemos usar a tabela 1 novamente:
Passo 4
Item c) Podemos usar a leitura do manômetro para determinar as pressões locais. A pressão na garganta mais a coluna de mercúrio devem ser iguais a pressão em (1):
Não possuímos os valores de e . Então vamos recorrer à tabela 1 para relacioná-los as pressões de estagnação.
Perceba que a garganta está à montante, e que na garganta o número de Mach é igual a um.
Podemos utilizar os valores imediatamente a jusante da onda de choque para relacionar as pressões:
Aplicamos esses valores na equação do manômetro:
Ainda continuamos com dois valores desconhecidos. Então vamos usar a tabela 2 e conseguir uma relação para as pressões de estagnação
Agora temos um sistema de equações para resolver:
Aplicando a segunda equação na primeira:
E agora resolvemos a segunda equação: