Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 27
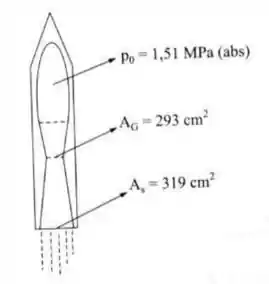
A velocidade dos gases na saída de um foguete é 2000 m/s. A pressão na câmara de combustão é 1,51 Mpa (abs). Sabendo que a área de saída é e que o escoamento é totalmente isentrópico, determinar a pressão e a temperatura dos gases na saída do foguete e a força de propulsão. Supor que as propriedades dos gases coincidam com as do ar.
Passo 1
A área na garganta é a própria área crítica:
Pela tabela 1 temos uma situação subsônica e outra supersônica.
Mas como se trata de um foguete, é razoável aceitar que este é um escoamento supersônico. De agora em diante seguiremos com essa consideração.
Passo 2
Utilizando a velocidade, podemos determinar a temperatura:
Pela tabela 1 podemos determinar a pressão
A densidade pode ser determinada pela lei dos gases:
Passo 3
A força pode ser determinada utilizando a vazão mássica e a velocidade:
Substituindo a fórmula da vazão mássica:
Aplicando os valores: