Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 34
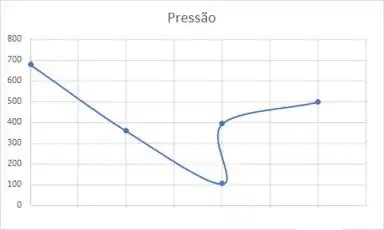
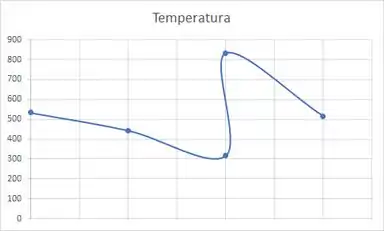
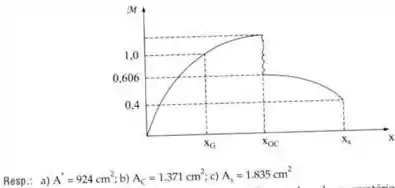
No ensaio de um bocal convergente/divergente, utilizou-se o ar contido num reservatório de grandes dimensões à pressão de e à temperatura de 533 K. Para uma vazão em massa de , obteve-se o diagrama da figura. Determinar:
- A área crítica
- A área onde ocorre a onda de choque
- A área da seção de saída
Esboçar os diagramas e , especificando os valores de e nas seções de entrada, da garganta, da onda de choque e de saída do bocal.
Passo 1
Item a) A questão nos fornece a vazão mássica. Então usando a velocidade e a densidade na garganta poderemos calcular a área crítica. Vamos usar a tabela um para determinar a pressão e a temperatura, depois usamos isso para determinar a densidade e a velocidade.
Note também que a pressão e temperatura no reservatório são as propriedades estáticas à montante do escoamento. Então podemos usar a seção da garganta (que está à montante) para determinar:
Agora podemos determinar a densidade pela lei dos gases:
E determinar a velocidade:
Finalizamos o item calculando a área através da vazão:
Lembrando que a área crítica é igual a área da garganta
Passo 2
Item B) Olhando o diagrama, percebemos que a onda de choque ocorre no ponto . Como já possuímos a área crítica, se determinarmos o número de mach imediatamente a montante deste ponto poderemos usar a tabela 1 para determinar a área.
O diagrama nos dá o valor do número de mach à jusante da onda de choque. Vamos usar isso na tabela 2 para determinar o número de Mach à montante:
Agora com o número de mach à montante, vamos usar a relação entre áreas
Aplicando o valor da área crítica:
Observe que como é o mesmo ponto, a área imediatamente à jusante tem o mesmo valor:
Passo 3
Item c) Calcular a área de saída é fácil! Primeiro vamos determinar a área crítica à jusante
Agora vamos usar o número de Mach da saída para determinar a área da saída
Passo 4
Vamos usar pegar as propriedades de todos os pontos para gerar os diagramas:
Seção de entrada: Nesta seção os valores são iguais aos valores estáticos à montante.
Seção da garganta: Já calculamos as propriedades da garganta
Seção da onda de choque imediatamente à montante: Vamos usar o número de Mach e a tabela 1
Seção da onda de choque imediatamente à jusante:
Vamos aproveitar esse momento para calcular a pressão de estagnação à jusante:
Seção de saída do bocal:
Utilizando o Excel vamos plotar os dados:
