Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas - Ex. 69
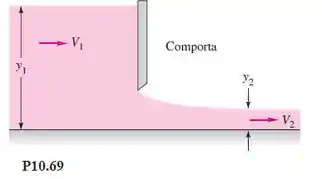
É dado um escoamento em um canal de grande largura b sob uma comporta de fundo, como mostra a Figura P10.69. Considerando escoamento permanente sem atrito com energia cinética desprezível a montante, deduza uma fórmula para a vazão adimensional como uma função da relação . Mostre por diferenciação que a vazão máxima ocorre em .
Passo 1
Lets go pra mais uma, cara!
Vamo lá, pegamos primeiro a equação de energia, já desconsiderando a energia cinética, assim:
Bora rearranjar isso ai e multiplicar por , assim:
Diferenciando em relação a e igualando a zero para encontrar o máximo, teremos:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Na Figura P10.69, suponha que y 1 = 1,4m e a comporta esteja levantada de maneira que a abertura seja de 15 cm. Calcule a vazão resultante por unidade de largura e a profundidade a jusante.
Na Figura P10.69, seja y 1 = 95c mey 2 = 50c m . Calcule a vazão por unidade de largura se a energia cinética a montante for (a) desprezada e (b) incluída.
O espetacular extravasamento de água na foto de abertura do capítulo escoa por meio de uma gigantesca comporta de fundo. Suponha que a comporta tenha 23 m de largura e a abertura tenha 8 m de altura.
Com relação à Figura P10.69, mostre que, para escoamento sem atrito, a velocidade a montante pode ser relacionada com os níveis da água pela relação: V 1 = 2 g y 1 - y 2 K 2 - 1 em que K = y 1 / y 2 .