Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 14.Problemas - Ex. 63

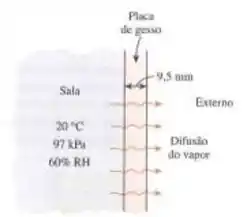
A difusão do vapor de água através de placas de gesso e sua condensação no isolamento da parede em clima frio são preocupantes, pois reduzem a eficácia do isolamento. Considere uma casa mantida a 20°C e 60% de umidade relativa no local onde a pressão atmosférica é de 97 kPa. O interior das paredes está acabado com placas de gesso de 9,5 mm de espessura. Considerando que a pressão de vapor na face externa das paredes é zero, determine a quantidade máxima de vapor de água que será difundida por uma seção de 3   m ×   8   m de parede durante um período de 24 horas. A permeação de placas de gesso de 9,5 mm de espessura ao vapor de água é de 2,86 × 10 - 9 k g s · m 2 · P a .

Passo 1

Booom galeraa, vamos continuar, ok?

Respirem fundo e vamos lá !!

Nós queremos a quantidade de vapor que flui através da superfície da parede ao longo de um período de tempo, o que nós vamos precisar achar ?

A vazão mássica do vapor, não é?

Bora ver a fórmula?

m v ˙ = P A B A . P v , 1 - P v , 2 L

O que sabemos?

L = 9,5   m m = 0,0095   m

A = 3   m ×   8   m = 24   m ²

P v , 2 = 0   P a

Ixiii!!

Vamos ver o que mais podemos descobrir?

Quando a temperatura e a umidade relativa são conhecidas, a pressão do vapor é calculada como:

P v a p o r = ∅ P s a t u r a ç ã o

Quando:

T 1 = 2 0 ° C →   P s a t ,   1 = 2339   P a  

E:

∅ = 6 0 % = 0 , 6

Agora podemos achar a pressão de vapor:

P v , 1 = 0 , 6 × 2339   P a = 1403,4   P a

Passo 2

Agora o único dado que falta é a permeabilidade!

Se lembram da fórmula?

P A B = M L

Onde M é a permeação e L a espessura!

Sabemos que quando:

L = 9,5   m m = 0,0095   m

M = 2,86 × 10 - 9 k g s · m 2 · P a

Substituindo:

P A B = 2,86 × 10 - 9 k g s · m 2 · P a 0,0095   m = 2,717 × 10 - 1 1 k g s . m . P a

Com isso nós podemos achar a vazão mássica:

m v ˙ = 2,717 × 10 - 11 k g s . m . P a 24   m . 1403,4   P a - 0   P a 0,0095   m

m v ˙ = 9,633 × 10 - 5 k g s

Acabamos?

Que nada né!

Passo 3

Se nós queremos a massa após um período de 24 h vamos precisar usar a seguinte fórmula:

m v = m v ˙ × ∆ t

Vamos substituir?

m v = 9,633 × 10 - 5 k g s × 3600   s   1   h × 24   h

m v = 8,32   k g

Sendo assim, nesta seção nós temos 8,32   k g de umidade atravessando a parede !

Legal, não foi?

Resposta

m v = 8,32   k g

Ver Outros Exercícios desse livro