Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 12
Dois aviões equipados com sensores de ondas de pressão deslocam-se na mesma trajetória, um contra o outro, com velocidades de (avião 1) e (avião 2). No local do movimento, e .
- Qual dos dois sensores resgistrará primeiro a presença do outro avião?
- Sabendo que o raio de propagação da onda registrada pelo sensor é 14800 m, qual é a distância entre os aviões, no instante em que o sensor resgistra a presença do outro.
- Sabendo que o tempo mínimo de manobra para mudar a trajetória do avião (1) é 15 s e do avião (2) é 5 s, haverá colisão?
Passo 1
Ao viajar, os aviões causam uma onda de choque no ar. Esta onda de choque viaja na velocidade do som, então o avião 1 (que é supersônico) viaja à frente da onda de choque gerada por ele. Já o avião 2, que é subsônico, viaja atrás da própria onda de choque.
Então, como esquematizado na figura, o avião 1 será atingido primeiro pela onda de choque 2, e irá detectar a presença do avião 2.
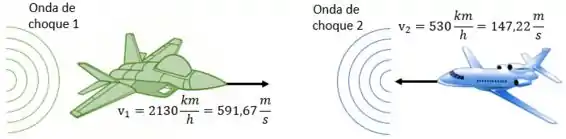
Passo 2
Primeiro, vamos calcular a velocidade de propagação no meio:
Para calcular o tempo, basta dividir o raio de atuação da onda de choque pela velocidade de propagação:
Assim, a distância entre os aviões, é a diferença entre o raio da onda de choque, e a distância percorrida pelo avião 2 no tempo :
Passo 3
A velocidade relativa entre os aviões é:
Então o tempo para a colisão é:
Tempo suficiente para o avião 2 desviar.
Resposta
- Não haverá colisão