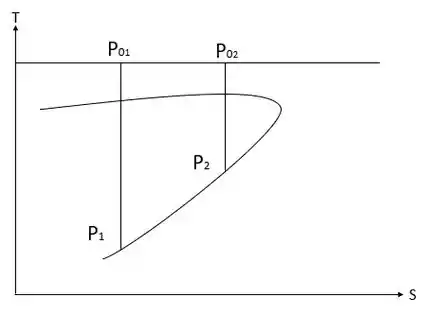
Um duto liso de área constante () deve ser alimentado por um bocal convergente-divergente, a partir de um tanque contendo ar a e . Uma operação livre de choque é desejada. O número de Mach na entrada do duto deve ser 2,1 e o número de Mach na saída deve ser 1,4. O conjunto todo será isolado termicamente. Determine (a) a pressão requerida na saída do duto, (b) o comprimento requerido do duto e (c) a variação na entropia específica. Mostre os pontos dos estados de estagnação e estáticos e a linha do processo em um diagrama .

Assumindo que possuímos um fluxo isentrópico no bocal:

Sendo:

.

Temos:

Calculando a massa específica pela equação dos gases ideais:

Substituindo os valores:

Como a vazão mássica permanece constante, pela continuidade, temos:

Calculando :

Letra b)

Com , na tabela de funções de fluxo de linha Fanno, temos:

Com :

Como:

Assim, sabemos que o fator de atrito é uma função do número de Reynolds em tubos lisos.

A viscosidade dinâmica pode ser calculada pela equação de Sutherland:

Sendo:

;

.

Temos:

Então o número de Reynolds se dá:

Substituindo os dados:

Obtendo no Diagrama de Moody com Tubo Liso:

Então:

Letra c)

A variação na entropia específica se dá:

Sendo:

.

Temos:

Mostre os pontos dos estados de estagnação e estáticos e a linha do processo em um diagrama .