Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 2.Problemas - Ex. 65

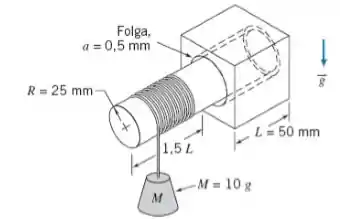
Um eixo circular de alumínio montado sobre um mancal de sustentação estacionário é mostrado. A folga simétrica entre o eixo e o mancal está preenchida com óleo SAE 10W30 a T = 30ºC. O eixo é posto em rotação pela massa e corda a ele conectadas. Desenvolva e resolva uma equação diferencial para a velocidade angular do eixo como função do tempo. Calcule a velocidade angular máxima do eixo e o tempo requerido para ele atingir 95% dessa velocidade.

Passo 1

Fala aí galera, vamos para mais um problema de mecânica dos fluidos.

Aplicando a soma de torques e a soma de forças:

Sabemos que:

Logo:

Para a soma de torques:

Entretanto, sabemos que:

Para um fluido newtoniano com perfil linear:

O foco aqui não é a resolução de EDO, logo, vamos pular esta parte. Resolvendo a equação e substituindo os resultados encontraremos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem vai a um açougue tradicional comprar um filé para o jantar. Ele encontra uma peça de 12o z ( 1I b m = 16o z ) por $ 3,15 . Vai então ao supermercado vizinho e acha uma peça de 320g de qualida

Resolva o sistema de três equações com três incógnitas usando o EES: 2 x - y + z = 5 3 x 2 + 2 y = z + 2 x y + 2 z = 8

A força de reação movida por um motor a jato para impulsionar um aeroplano para frente é chamada de empuxo e o empuxo desenvolvido por um motor de um Boening 777 é de cerca de 85.000I b f . Expresse e

Resolva o sistema de três equações com três incógnitas usando o EES: x 2 y - z = 1 x - 3 y 0,5 + x y = - 2 x + y - z = 2

Determine uma raiz real positiva dessa equação usando o EES: 2 x 3 - 10 x 0,5 - 3 x = - 3