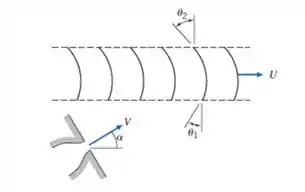
Considere uma série de pás curvas atingidas por um jato contínuo de água com velocidade constante, . O jato sai de um bocal de de diâmetro e as pás se movem com velocidade constante, . Note que toda a vazão em massa do jato atravessa as pás. A curvatura das pás é descrita pelos ângulos e , conforme mostrado. Avalie o ângulo do bocal, , requerido para assegurar que o jato penetre tangentemente à borda de ataque de cada pá. Calcule a força que deve ser aplicada para manter a velocidade das pás constante.

Para analisar o ângulo do bocal, , requerido para assegurar que o jato penetre tangentemente à borda de ataque de cada pá, desenharemos um sistema com vetores e ângulos:

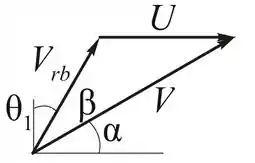
Sendo:

;

;

.

Pelas relações trigonométricas, temos que:

Assim:

Tendo

;

;

.

Conseguimos obter :

De acordo com o desenho:

Então:

Com o ângulo obtido, conseguimos obter o valor de :

Pelas considerações feitas no passo 1, utilizaremos a seguinte equação da quantidade de movimento:

Como estamos analisando um sistema , temos:

Não há forças de campo atuando no sistema, então :

Não temos a variação das propriedades com o tempo, então:

Assim:

Sendo que:

Então:

Desse modo, a força resultante se dá:

Para o fluxo de entrada, possuem uma inclinação de 180°, então .

Aqui, indica a velocidade relativa do fluxo de entrada, já , a velocidade relativa do fluxo de saída para as mesmas condições.

Onde:

;

.

Então:

Sendo:

;

;

.

;

;

.

Temos: