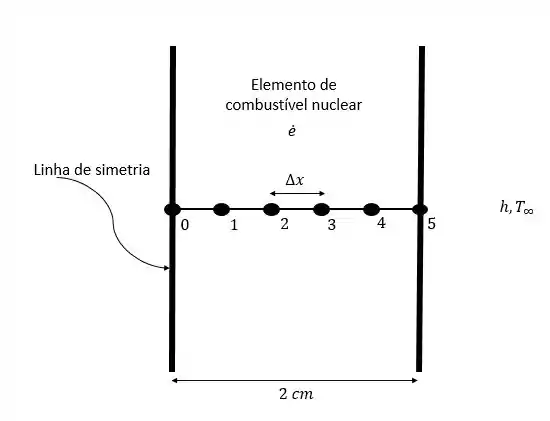
Um elemento de combustível () que pode ser modelado como uma parede plana, tem espessura de . O elemento de combustível gera de calor uniformemente. Ambas as superfícies laterais do elemento de combustível são resfriadas por um líquido a uma temperatura de , e o coeficiente de transferência de calor por convecção é de . Use espaçamento nodal uniforme de e faça uso da linha simétrica no centro da parede plana e determine (a) as equações de diferenças finitas e (b) temperaturas nodais, resolvendo as equações.

Primeiramente, iremos assumir algumas considerações para simplificar o problema. São elas:

• Transferência de calor através do elemento de combustível nuclear é permanente e unidimensional.
• Propriedades térmicas são constantes.
• Transferência de calor por radiação é desprezível.

De posse dessas características, podemos entender melhor o sistema com o qual a questão pretende trabalhar.

(a) O espaçamento nodal é dado no valor de , então, o número de nós é:

Temos temperaturas nodais desconhecidas, portanto precisaremos de equações para determinar cada uma delas. A equação de diferenças finitas para o nó na superfície esquerda, na linha de simetria, é obtida pela aplicação do balanço de energia sobre o elemento de volume finito sobre o nó (é importante saber que a linha de simetria funciona como uma superfície isolada):

Os nós e são nós interiores, então podemos usar a relação geral de diferenças finitas, expressa como:

Assim como no nó , o nó é obtido pela aplicação do balanço de energia sobre o elemento de volume finito sobre o nó, com a diferença de que este nó está sujeito à convecção, logo:

Então:

Nó :

Nó :

Nó :

Nó :

Nó :

Nó :