O empuxo de uma hélice de embarcação deve ser medido durante testes de “água­aberta” a diversas velocidades angulares e velocidades à frente (“velocidades de avanço”). Supõe­se que o empuxo, , depende da massa específica da água, , do diâmetro da hélice, , da velocidade de avanço, , da aceleração da gravidade, , da velocidade angular, , da pressão no líquido, , e da viscosidade do líquido, . Desenvolva um conjunto de parâmetros adimensionais para caracterizar o desempenho da hélice. (Um dos parâmetros resultantes, é conhecido como a velocidade de avanço de Froude.)

Para resolver essa questão usaremos o teorema pi de Buckingham. Onde encontramos que o número de parâmetros é:

Selecionando as dimensões primárias

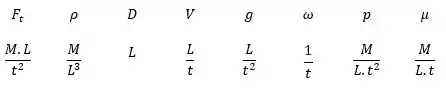
E os parâmetros repetidos:

Então nós temos grupos sem dimensão. Configurando as seguintes equações dimensionais:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Para o segundo grupo temos:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Para o terceiro grupo temos:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Para o quarto grupo temos:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Para o quinto grupo temos:

Somando os expoentes:

Temos que a solução do sistema é:

Então:

Verificando usando as dimensões :