Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 13.Problemas - Ex. 101

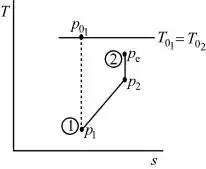
Ar escoa adiabaticamente de um reservatório, onde T = 60 ° C e p = 600   k P a   ( a b s ) , atrave´s de um bocal convergente-divergente com A e / A t = 4,0 . Um choque normal ocorre ond M = 2,42 . Considerando escoamento isentrópico antes e depois do choque, determine a contrapressão a jusante do bocal. Esboce a distribuição de pressão.

Passo 1

Pela tabela de funções de fluxo isentrópico, obtemos a razão entre as pressões pelo número de Mach  M 1 = 2,42 utilizando uma interpolação:

p 1 p 0 1 = 0,1278 + 2,42 - 2 2,5 - 2 ⋅ 0,05853 - 0,1278

p 1 p 0 1 = 0,0696

Temos que:

p 0 1 = 600   k P a   ( a b s ) .

Então:

p 1 600 = 0,0696

p 1 = 41,76   k P a

De volta a tabela de funções de fluxo isentrópico, obtemos a razão entre as áreas pelo número de Mach  M 1 = 2,42 utilizando uma interpolação:

A 1 A * = 1,68 8 + 2,42 - 2 2,5 - 2 ⋅ 2,637 - 1,68 8

A 1 A * = 2,485

Agora, na tabela de funções normais do fluxo de choque, obtemos o número de Mach, M 2 , após o choque utilizando uma interpolação:

M 2 = 0,5774 + 2,42 - 2 2,5 - 2 ⋅ 0,5130 - 0,5774

M 2 = 0,5233

Passo 2

Na mesma tabela, obtemos a razão das pressões de estagnação pelo número Mach, M 1 , utilizando uma interpolação:

p 0 2 p 0 1 = 0,7209 + 2,42 - 2 2,5 - 2 ⋅ 0 , 4990 - 0,7209

p 0 2 p 0 1 = 0,5345

Substituindo p 0 1 :

p 0 2 600 = 0,5345

p 0 2 = 320,7   k P a

Continuando na tabela de funções normais do fluxo de choque, oobtemos a entre as pressões pelo número de Mach, M 1 , utilizando uma interpolação:

p 2 p 1 = 4,5 + 2,42 - 2 2,5 - 2 ⋅ 7,125 - 4,5

p 2 p 1 = 6,705

Substituindo p 1 :

p 2 41,76   = 6,705

p 2 = 280   k P a

Passo 3

Agora, voltando na tabela de funções de fluxo isentrópico, obtemos a razão das áreas pelo número de Mach, M 2 , utilizando uma interpolação:

A 2 A 2 * = 1,34 + 0,8233 - 0,5 1 - 0,5 ⋅ 1 - 1,34

A 2 A 2 * = 1,32

Como A 1 = A 2 , então:

A 2 A 2 * = A 1 A 2 *

Calcuando a razãoda área de saída para a área crítica da seção 2 após o choque normal:

A s a í d a A 2 * = A s a í d a A 1 * ⋅ A 1 * A 1 ⋅ A 1 A 2

` Substituindo:

A s a í d a A 2 * = 4,0 ⋅ 1 2,485 ⋅ 1,32

A s a í d a A 2 * = 2,125

Passo 4

Calculando o número de Mach na saída:

A s a í d a A 2 * = 1 M s a í d a 1 + k - 1 2 M s a í d a 2 k + 1 2 k + 1 2 ( k - 1 )

Sendo:

k = 1,4 .

Temos:

2,125 = 1 M s a í d a 1 + 1,4 - 1 2 M s a í d a 2 1,4 + 1 2 1,4 + 1 2 ( 1,4 - 1 )

M s a í d a = 0,286

Calculando a razão entre a pressão de estagnação, p 0 2 e a pressão de saída, p s a í d a :

p 0 2 p s a í d a = 1 + k - 1 2 M s a í d a 2 k k - 1

Substituindo os dados:

p 0 2 p s a í d a = 1 + 1,4 - 1 2 ⋅ 0,286 2 1,4 1,4 - 1

p 0 2 p s a í d a = 1,058

Como as pressões de saída e de retorno são as mesmas, calculamos a contrapressão:

p s a í d a = p r e t o r n o

p r e t o r n o p 0 2 = 1 1,058

p r e t o r n o p 0 2 = 0,945

Substituindo p 0 2 :

p r e t o r n o 320,7 = 0,945

p r e t o r n o = 303,06   k P a

Passo 5

Esboçando a distribuição de pressão:

Resposta

p r e t o r n o = 303,06   k P a

Ver Outros Exercícios desse livro