Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 12.Exercício - Ex. 38
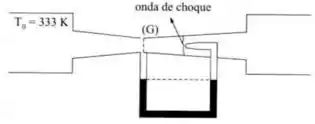
O ar escoa por um convergente/divergente. Numa seção do escoamento, forma-se uma onda de choque normal. As condições são tais que, no manômetro ligado ao tubo de Pitot da figura, o nível do mercúrio é igual nos dois ramos. Qual é a velocidade na seção a jusante da onda de choque?
Passo 1
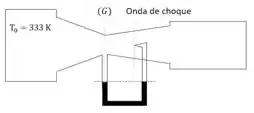
A igualdade entre o manômetro e o tubo de pitot quer dizer que: A pressão manométrica no ponto (G) é igual a pressão estática à jusante da onda de choque
Em outras palavras isso quer dizer que a relação entre as pressões é tal que:
Passo 2
Bem, sabemos que a garganta é o ponto crítico onde o número de Mach é igual a um, podemos então encontrar o valor da relação de pressão
Então:
Passo 3
Agora podemos usar a Tabela 2:
Com o valor do número de Mach à jusante, vamos usar a Tabela 1
Calculamos agora à temperatura:
Passo 4
Finalizamos a questão calculando a velocidade