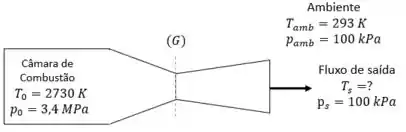
Um pequeno foguete é testado num banco de provas. A saída dos gases de combustão é feita por um divergente, em que os gases sofrem uma expansão total até a pressão ambiente. A temperatura e a pressão na câmara de combustão são, respectivamente, 2730 K e 3,4 Mpa (abs) e a câmara de combustão é considerada um reservatório de grandes dimensões. O consumo total de oxidante e combustível é 4,5 kg/s. Supondo o escoamento isentrópico e dados k=1,4 e , determinar

1. A força de propulsão indicada no dinamômetro;
2. A área da seção de saída
3. A área de seção crítica.

Observe que há câmara de combustão é um reservatório de grandes dimensões com velocidade do ar igual a zero. Então, podemos considerar que a pressão e temperatura na câmara de combustão são iguais a temperatura e pressão de estagnação.

Observe também que, ao sair do convergente a pressão do fluxo se iguala a pressão ambiente. Mas a temperatura do fluxo ainda é desconhecida.

A força que será medida pelo dinamômetro é resultado da saída rápida de gás ao fim da turbina, e pode ser computado como:

A questão já nos fornece o fluxo de massa, então vão calcular a velocidade na saída. Mas para isso precisaremos da temperatura e do número de Mach na saída, valores que podem ser obtidos pela tabela 1. Primeiro calculamos a relação entre pressão:

Agora consultamos a tabela:

E podemos calcular velocidade do fluxo de saída:

Então a força do foguete é: