Para escoamento bidimensional constante sobre uma placa plana isotérmica a uma direção , expresse as condições de contorno para os componentes de velocidade e , e a temperatura na superfície da placa e no bordo da camada limite.
Passo 1
Esta é a nossa situação:
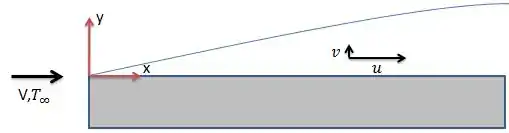
Um fluido escoando sobre uma placa plana isotérmica de temperatura .
Passo 2
Agora vamos lembrar da hipótese do não-deslizamento. Em poucas palavras esta teoria diz que a camada de fluido em contato com a superfície assume instantaneamente as propriedades da superfície. Ou seja, se a placa está parada () e possui temperatura , a camada de fluido imediatamente acima da placa também possui e temperatura .
Tendo isso em mente,vamos aplicar a hipótese do não-deslizamento para montar as primeiras condições de contorno.
Para o fluido em contato com a superfície da placa ():
Passo 3
Agora vamos considerar a porção de fluido que não é afetada pela camada limite. Para isso, podemos pensar em dois casos: (1) o fluido ainda não entrou em contato com a placa () ou (2) o fluido está a uma distância muito grande da placa e não sente os efeitos da camada limite ().
Para as condições são:
Para as condições de contorno são:
Resposta
Ei, a resposta está no passo a passo :)