Para o escoamento isentrópico de ar, em uma seção de um canal onde , , e . Determine o número de Mach e a vazão mássica. Em uma seção a jusante, a temperatura é 137°C e o número de Mach é 0,75. Determine a área transversal e a pressão nessa seção. Esboce a forma do canal.

Pela equação de gás ideal:

Sendo:

;

;

;

Então:

Calculando a vazão mássica na seção 1:

Sendo:

;

;

.

Temos que:

Dividindo as equações, temos que:

Temos:

;

;

;

;

Para encontrar a densidade na seção 2:

Temos:

;

;

.

Para encontrar a velocidade no estado 2:

Como temos a vazão mássica constante:

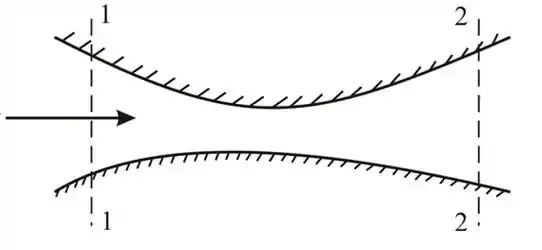
A forma do canal se mostra como na figura abaixo: