Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 75
Uma esfera com 30 mm de diâmetro inicialmente a 800 K é resfriada em um grande banho, mantido a uma temperatura constante de 320 K e com um coeficiente de transferência de calor por convecção de 75 W/(m2 · K). As propriedades termofísicas do material da esfera são: ρ = 400 kg/m3, c = 1600 J/(kg · K) e k = 1,7 W/(m · K).
(a) Mostre, de maneira qualitativa em coordenadas T – t, as temperaturas no centro e na superfície da esfera em função do tempo.
(b) Calcule o tempo necessário para a superfície da esfera atingir a temperatura de 415 K.
(c) Determine o fluxo térmico (W/m2) na superfície externa da esfera no instante determinado na parte (b).
(d) Determine a energia (J) que foi perdida pela esfera durante o processo de resfriamento até a sua temperatura na superfície atingir 415 K.
(e) No tempo determinado na parte (b), a esfera é rapidamente removida do banho de resfriamento e coberta por uma camada de um isolante térmico perfeito, de tal forma que não há mais perda de calor pela superfície da esfera. Qual será a temperatura da esfera após transcorrido um longo período de tempo?
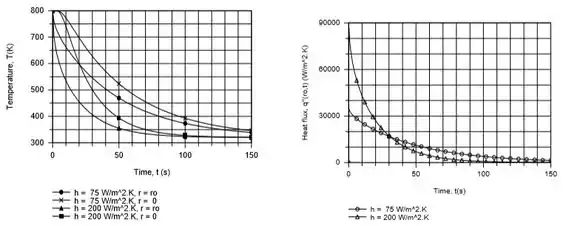
(f) Calcule e represente graficamente os históricos das temperaturas no centro e na superfície da esfera para o período 0 ≤ t ≤ 150 s. Que efeito tem um aumento no valor do coeficiente de transferência de calor por convecção para h = 200 W/(m2 · K) sobre os históricos representados anteriormente? Para h = 75 e 200 W/(m2 · K), calcule e represente o fluxo térmico na superfície em função do tempo para .
Passo 1
Vamo lá galera! (a) Calcular o número Biot para determinar se a esfera se comporta como objeto espacialmente isotérmico,
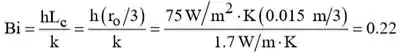
Portanto, existem gradientes de temperatura na esfera e aparece como mostrado acima.
(b) A solução exata pode ser usada para encontrar quando . Assumimos que a aproximação de um prazo é válida e verificamos mais tarde. Portanto, com
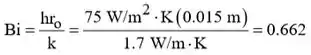
Da tabela 5.1, logo,
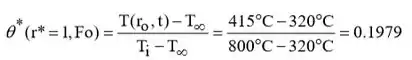
E da equação 5.53b pode ser resolvido para theta,
Então a Equação 5.53c pode ser resolvida para Fo:
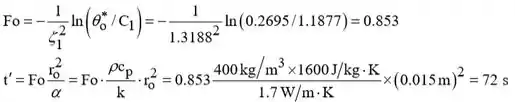
Passo 2
(c) O fluxo de calor na superfície externa no momento ′t é dado pela lei de Newton de resfriamento,
A maneira pela qual é calculado indica que a energia está saindo da esfera.
(d) A energia perdida pela esfera durante o processo de resfriamento de a pode ser determinada a partir da Equação 5.55:
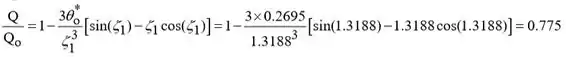
A perda de energia pela esfera,
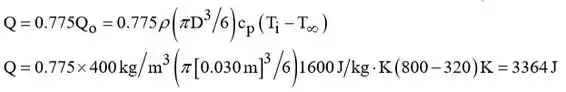
Passo 3
(f) Utilizando o Modelo de Condução Transiente IHT para uma Esfera, foram gerados os seguintes resultados gráficos,
