Na Seção 5.2 observamos que o valor do número de Biot influencia de forma significativa a natureza da distribuição de temperaturas em um sólido durante um processo condutivo transiente. Reforce o seu entendimento desse conceito importante usando o modelo IHT uma rotina computacional para condução unidimensional transiente para determinar a distribuição radial de temperaturas em um bastão de aço inoxidável (k = 15 W/(m · K), ρ = 8000 kg/m3, cp = 475 J/(kg · K)), com 30 mm de diâmetro, quando ele é resfriado de uma temperatura inicial uniforme de 325°C por um fluido a 25°C. Para os valores a seguir do coeficiente de transferência de calor por convecção e os tempos designados, determine a distribuição radial de temperaturas: h = 100 W/(m2 · K) (t = 0, 100, 500 s); h = 1000 W/(m2 · K) (t = 0, 10, 50 s); h = 5000 W/(m2 · K) (t = 0, 1, 5, 25 s). Prepare um gráfico para cada coeficiente convectivo, no qual a temperatura será representada como uma função do raio adimensional nos tempos designados.

Vamo lá galera! O modelo IHT é baseado na solução exata para a equação de calor, Eq. 5,50. Os resultados são plotados da seguinte forma,

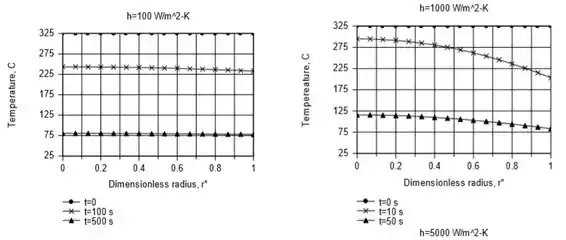
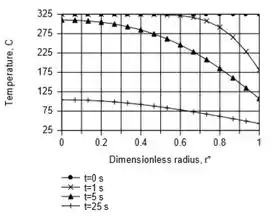
Para , e como esperado, a distribuição de temperatura é quase uniforme em toda a haste. Para as variações de temperatura dentro da haste não são desprezíveis. Neste caso, a diferença de temperatura entre a linha central e a superfície é comparável à diferença de temperatura entre a superfície e o fluido. Para as variações de temperatura dentro da haste são grandes e é substancialmente maior do que