Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 7.Exercício - Ex. 26

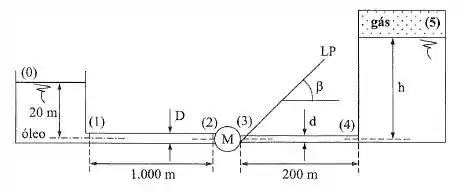
Na instalação da figura, determinar:

a) a altura h ;

b) o tipo de máquina;

c) a potência da máquina se η M = 70 %

Dados: Q = 31,4   L / s ; tg ⁡ β = 0,2 ; γ = 8000   N / m 3 ; ν = 10 - 4   m 2 / s ; k s 1 = 16 ; L e q 4 = 20   m ; p 5 = 32   k P a ; D = 20   c m ; d = 10   c m .

Passo 1

Beleza, a primeira coisa é notar que devido à inclinação da LP, o sentido do escoamento se dá de (5) para (1). Agora, como temos o valor da tg ⁡ β e sabemos que a diferença de altura nesse trecho corresponde a perda de carga distribuída, podemos escrever:

tg ⁡ β = h f 4,3 L 4,3

Substituindo os valores conhecidos:

0,2 = h f 4,3 200 → h f 4,3 = 40   m

Vamos agora encontrar a velocidade do escoamento, que devido a uniformidade da seção do tubo durante todo o trajeto, é constante:

Q = v A → v = Q A = Q π d 2 4 = 31,4.10 - 3 π 0,1 2 4 → v = 4   m / s

Agora podemos encontrar o valor do fator de atrito f entre os pontos 4 e 3 através da fórmula da perda de carga distribuída, que é dada por:

h f 4,3 = f 4,3 L v 2 2 g d

Substituindo os valores conhecidos, temos:

40 = f 4,3 200 4 2 2 10 0,1 → f 4,3 = 0,025

Passo 2

Agora podemos encontrar o valor da perda de carga entre o trecho (5) a (3), que será a perda distribuída nesse trecho, já que temos o comprimento equivalente da perda localizada em (4), então, temos:

H p 5,3 = h f 5,3 = f 4,3 L v 2 2 g d

Substituindo os valores conhecidos:

H p 5,3 = 0,025 220 4 2 2 10 0,1 → H p 5,3 = 44   m

Com esse valor, podemos aplicar o equilíbrio de energia entre os pontos 5 e 3:

H 5 = H 3 + H p 5,3

v 5 2 2 g + p 5 γ + z 5 = v 3 2 2 g + p 3 γ + z 3 + H p 5,3

Substituindo os valores conhecidos, temos:

0 2 2 g + 32.10 3 8000 + h = 4 2 2 10 + 0 + 0 + 44 → h = 40,8   m

Passo 3

Agora, para a letra b), como a máquina precisa elevar a pressão do sistema, conforme vimos no passo 2, então sabemos que ela só pode ser uma bomba.

Passo 4

Agora para encontrar o valor da potência da bomba, precisamos primeiro encontrar o valor de sua carga. Então, para começar, vamos encontrar a velocidade do escoamento no trecho de (2) para (1), sabendo que a vazão foi dada no enunciado, temos:

Q = v 2,1 A 2,1 → v 2,1 = Q A 2,1 = Q π D 2 4 = 31,4.10 - 3 π 0,2 2 4 → v 2,1 = 1   m / s

Então agora vamos calcular o número de Reynolds para o escoamento:

R e 2,1 = v 2,1 D ν = 1 0,2 10 - 4 → R e 2,1 = 2000

Sabemos que para esse valor de Reynolds podemos considerar o escoamento como sendo laminar, então, podemos encontrar o fator de atrito f através da equação 7.11 apresentada nessa seção:

f 2,1 = 64 R e 2,1 = 64 2000 → f 2,1 = 0,032

Com o fator de atrito podemos encontrar a perda de carga distribuída nesse trecho:

h f 2,1 = f 2,1 L 2,1 v 2,1 2 2 g D = 0,032 1000 1 2 2 10 0,2 → h f 2,1 = 8   m

Vamos também encontrar o valor da perda de carga localizada no ponto 1 através de:

h s 1 = k s 1 v 2,1 2 2 g = 16 1 2 2 10 → h s 1 = 0,8   m

Com isso, podemos calcular a perda de carga total no trecho de (2) até (0):

H p 2,0 = h f 2,1 + h s 1 = 8 + 0,8 → H p 2,0 = 8,8   m

Passo 5

Agora vamos aplicar o equilíbrio de energia entre os pontos 3 e 0:

H 3 + H B = H 0 + H p 2,0

v 3 2 2 g + p 3 γ + z 3 + H B = v 0 2 2 g + p 0 γ + z 0 + H p 2,0

Substituindo os valores conhecidos, temos:

4 2 2 10 + 0 γ + 0 + H B = 0 2 2 g + 0 γ + 20 + 8,8 → H B = 28   m

E, finalmente, podemos aplicar a equação para a potência da bomba, que é dada por:

N B = γ Q H B η B = 8000 31,4.10 - 3 28 0,7 → N B = 10048   W

Resposta

h = 40,8   m

b o m b a

N B = 10048   W

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere novamente o escoamento através do cotovelo analisado no Exemplo 4.6. Usando as condições dadas, calcule o coeficiente de perda menor para o cotovelo.
Água escoa do tanque mostrado através de um tubo muito curto. Considere que o escoamento seja quase permanente. Estime a vazão no instante mostrado. Como você poderia melhorar o sistema de escoamento
Água escoa de um grande tubo, de diâmetro, de D 1 = 100m m , e entra em um tubo menor, de diâmetro D 2 = 500m m , por meio de um dispositivo reentrante. Encontre a perda de carga entre os pontos 1 e 2
Um tanque de água (aberto para a atmosfera) contém água a uma profundidade de 5 m. Um furo com diâmetro de 25 mm é perfurado no fundo. Modele o furo como de borda-viva, e estime a vazão (L/s) que sai
Água é bombeada através de um tubo comercial de aço carbono, de 230 mm de diâmetro, por uma distância de 6400 m, desde a descarga da bomba até um reservatório aberto para a atmosfera. O nível da água