Um esquema inovador para a dissipação de calor de uma série de circuitos integrados envolve a usinagem de canais de refrigeração no substrato cerâmico, no qual os chips são fixados. Os chips quadrados ( = 5 mm) são posicionados em linha acima de cada um dos canais, com passos longitudinal e transversal de = 20 mm. Água escoa através da seção transversal quadrada (W = 5 mm) de cada canal com uma velocidade média de = 1 m/s e suas propriedades podem ser aproximadas por ρ = 1000 kg/m³, = 4180 J/(kg · K), , k = 0,610 W/(m · K) e Pr = 5,8. Simetria na direção transversal obriga a existência de condições equivalentes em cada seção do substrato com comprimento e largura .

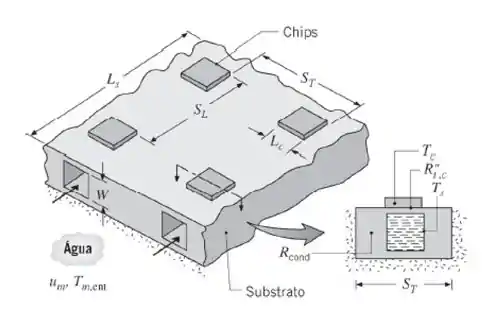
(a) Considere um substrato cujo comprimento na direção do escoamento é = 200 mm, o que implica um total de = 10 chips posicionados em linha acima de cada canal de escoamento. Com uma boa aproximação, todo o calor dissipado pelos chips acima de um canal pode ser considerado como transferido para a água que escoa através do canal. Se cada chip dissipa 5 W, qual é a elevação na temperatura da água que escoa através do canal?

(b) A resistência de contato entre o chip e o substrato é e a resistência à condução tridimensional na seção do substrato com dimensões é = 0,120 K/W. Se a água entra no substrato a 25 °C e o escoamento é plenamente desenvolvido, estime a temperatura dos chips e a temperatura na superfície do canal no substrato .

Agora para a letra (b), nós podemos analisar um circuito térmico que considera a temperatura dos chips e a temperatura média de saída no final e a temperatura na superfície do canal no substrato como intermediária, ou seja, podemos escrever o calor trocado como:

Então vamos começar calculando a temperatura média, como vimos no passo 1 que a diferença entre temperatura de entrada e saída é de 0,48 °C, então, como a temperatura de entrada foi dada como sendo de 25 °C, então a temperatura de saída será:

Então a temperatura média será:

Agora nós precisamos calcular as resistências térmicas para utilizar a equação descrita acima. Então, começando pela resistência de contato, temos:

Substituindo os valores conhecidos, lembrando que precisamos considrar os 10 chips, chegamos em:

Agora para a resistência de convecção, vamos precisar do coeficiente convectivo, que será dado pelo número de Nusselt, que por sua vez precisa do número de Reynolds para ser calculado. Então, para calcular Reynolds, precisamos calcular o diâmetro hidráulico da seção transversal, que será:

Então, com isso, Reynolds será:

Então, com o número de Reynolds encontrado no passo 2, podemos ver que o escoamento é turbulento, então, podemos encontrar o número de Nusselt pela correlação de Gnielinski, dada por:

Onde é dado por:

Então, substituindo os valores conhecidos no número de Nusselt, temos:

E, sabendo que o número de Nusselt se relaciona com o coeficiente convectivo da seguinte forma:

Substituindo os valores conhecidos, chegamos em:

Então, a resistência por convecção será:

Como nós já temos o valor da resistência a condução, podemos substituir os valores conhecidos na primeira parcela da equação lá do passo 2, teremos:

Agora, para a temperatura na superfície do canal no substrato pode ser obtida a partir da segunda parcela da equação da resistência térmica do passo 2, onde nós temos:

Substituindo os valores conhecidos, chegamos em: