Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 116
Determine o diâmetro do tubo que corresponde a 10% de redução no coeficiente de transferência de calor para coeficientes de acomodação térmica e de momento iguais a = 0,92 e = 0,89, respectivamente. Determine o espaçamento entre canais, a, que está associado à redução de 10% no h usando os mesmos coeficientes de acomodação. O gás é o ar a T = 350 K e a pressão atmosférica, tanto para o tubo quanto para as placas paralelas. O escoamento é laminar e plenamente desenvolvido, com fluxo na superfície constante.
Passo 1
Beleza! Vamos começar o exercício pegando as propriedades do ar na pressão atmosférica a uma temperatura de 350 K. Para isso, vamos recorrer a tabela A.4 do apêndice A, onde conseguimos as seguintes propriedades:
Agora, nós vamos recorrer à figura 2.8 vista no capítulo 2, onde poderemos pegar os valores dos diâmetros moleculares, então temos:
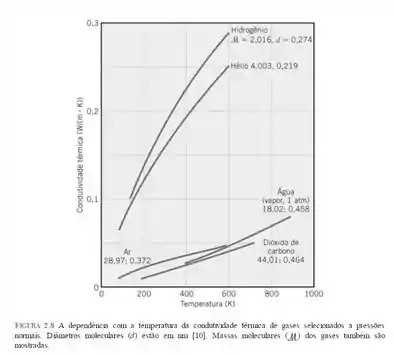
Com ela, podemos ver que o diâmetro molecular do ar será:
Agora, sabemos também que a constante de gás ideal para o ar é dada por:
Então, com isso, podemos calcular o calor específico a volume constante, onde teremos:
E, agora podemos calcular a razão entre os calores específicos, dado por:
Passo 2
Agora nós vamos recorrer à equação do livre percurso médio, dado pela equação 2.11, onde temos:
Sabendo que a constante de Boltzmann é dada por , então, substituindo os valores conhecidos nessa equação, teremos:
Agora, nós podemos encontrar o número de Nusselt através da equação 8.78a:
Onde temos dado por:
E que é dado por:
E, por sua vez, é dado por:
Passo 3
Então vamos começar calculando a expressão para :
Agora calculando a expressão para , temos:
E, por fim a expressão para :
Então, substituindo essas expressões na equação para Nusselt, temos:
Então, uma redução de 10% no coeficiente convectivo representa também uma redução de 10% no número de Nusselt. Então, sabendo que por padrão temos: , uma redução para 90% teremos:
Então, a equação anterior se torna:
Resolvendo essa equação com o auxílio de uma calculadora, chegamos no valor de diâmetro de:
Passo 4
Agora, da mesma forma que fizemos para o tubo, vamos fazer para o espaçamento entre canais , nesse caso, Nusselt é dado por:
Onde temos dado por:
E que é dado por:
E, por sua vez, é dado por:
Calculando esses itens novamente, da mesma forma que anteriormente, e aplicando uma redução de 10% no número de Nusselt, onde teremos então:
Dessa forma, utilizando uma calculadora para resolver a equação, teremos:
Nesse caso temos diâmetro hidráulico porque a seção não é redonda. E o espaçamento entre as placas é metade do diâmetro hidráulico, então teremos: