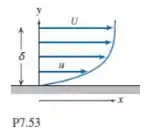
A velocidade do fluido, u, em qualquer ponto em uma camada-limite depende da distância, , do ponto acima da superfície, da velocidade da corrente livre, , e do gradiente de velocidade da corrente livre, , da viscosidade cinemática do fluido, , e daespessura da camada­limite, . Quantos grupos adimensionais são requeridos para descrever este problema? Determine: (a) dois grupos Π por inspeção, (b) um grupo Π que é um grupo­padrão em mecânica dos fluidos, e (c) quaisquer grupos Π remanescentes usando o teorema Pi de Buckingham.

Dois grupos que já podemos observar são:

e

Um grupo sem dimensão comum na mecânica de fluidos é (número de Reynolds)

Usando o procedimento Buckingham temos que o número de parâmetros é:

Selecionando as dimensões primárias

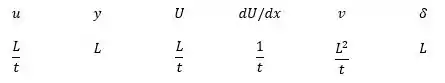
E os parâmetros repetidos:

Então nós temos grupos sem dimensão. Por inspeção temos:

Ah, e aqui não vai ser necessário verificar usando como dimensões primárias. \o/