Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 10.Problemas Abrangentes - Ex. 3
Estenda o Problema P10.72, cuja solução era V2 = 4,33 m/s. (a) Use a teoria de escoamento gradualmente variado para estimar a profundidade da água 10 m a jusante na seção (3) para (a) declive de 5°, de concreto sem acabamento, mostrado na Figura P10.72. (b) Repita os seus cálculos para um aclive (declividade adversa) de 5°. (c) Quando você descobre que a parte (b) é impossível com a teoria de escoamento gradualmente variado, explique por que e repita para uma aclive de 1°
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
Para o problema Problema P10.72, nós temos o s seguintes dados: , . Além disso, nós temos que .
Dessa forma, podemos utilizar a Equação 10.30, fornecida na página 719, pra calcular a profundidade crítica :
Como o canal é largo, podemos utilizar a formulação do Exemplo 10.9:
Sendo nossa condição inicial.
Pra resolver essa EDO, a gente tem que integrá-la numericamente considerando declividades de , e .
Nos próximos passos vamos usar o software Scilab pra resolver cada uma dessas situações.
Passo 2
Pra começar, vamos começar integrando a EDO numericamente pra . Fazendo isso, a gente encontra esse gráfico abaixo:
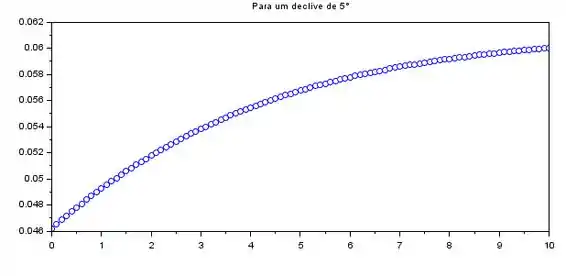
Como é possível ver pelo gráfico obtido na integração numérica, pra , teremos .
Passo 3
Agora, pra letra (b), assumimos pra . Obtemos assim o seguinte gráfico:
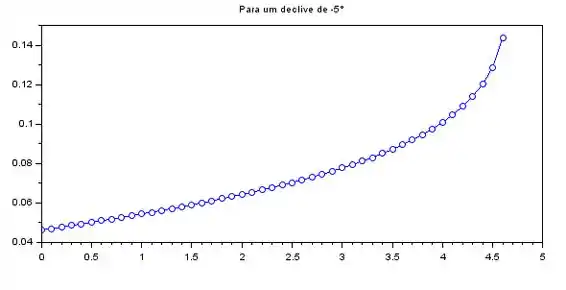
Como vocês podem ver, a profundidade vai se aproximando cada vez mais da profundidade crítica próximo de .
Por isso, quando tentamos resolver a EDO numericamente pra valores maiores que , nosso código dá erro.
Passo 4
Agora, pra finalizar a questão e resolver a letra (c), assumimos pra . Assim, obtemos assim o seguinte gráfico:
Como vocês podem ver, a profundidade vai se aproximando cada vez mais da profundidade crítica próximo de , então conseguimos resolver o problema pra distância que o enunciado pede.
Pronto, matamos a questão juntos!
Resposta
(a)
(b)
(c)